{x}
blog image

K Radius Subarray Averages

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

  • For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

 

Example 1:

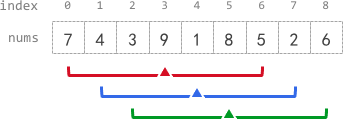
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

 

Constraints:

  • n == nums.length
  • 1 <= n <= 105
  • 0 <= nums[i], k <= 105

Solution Explanation: K Radius Subarray Averages

This problem asks to calculate the k-radius average for each index in the input array nums. The k-radius average for an index i is the average of elements within the range [i - k, i + k], inclusive. If this range extends beyond the array bounds, the average is -1.

The most efficient approach is using a sliding window technique. This avoids redundant calculations by iteratively updating the sum of the window as it slides across the array.

Algorithm:

  1. Initialization:

    • Create an ans array of the same size as nums, filled with -1. This will store the results.
    • Initialize a variable s to 0. This will keep track of the sum of elements within the current window.

  2. Iteration:

    • Iterate through nums using a loop. For each element nums[i]:
      • Add nums[i] to s.
      • Check if i is greater than or equal to 2k. This condition ensures the window has reached its full size (2k + 1).
      • If the condition is true:
        • Calculate the average: ans[i - k] = s // (2k + 1) (integer division).
        • Subtract nums[i - 2k] from s to remove the element that's leaving the window.

  3. Return:

    • Return the ans array.

Time and Space Complexity Analysis:

  • Time Complexity: O(n), where n is the length of nums. We iterate through the array once. The operations within the loop (addition, subtraction, division) are constant time.

  • Space Complexity: O(1) if we disregard the space used by the output array ans. The only extra space used is for the variables s and potentially a few loop counters, which is constant regardless of the input size. If we include ans, the space complexity becomes O(n).

Code Implementation (Python):

class Solution:
    def getAverages(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        ans = [-1] * n
        s = 0
        for i, x in enumerate(nums):
            s += x
            if i >= k * 2:
                ans[i - k] = s // (k * 2 + 1)
                s -= nums[i - k * 2]
        return ans

The code in other languages (Java, C++, Go, TypeScript) follows the same algorithmic structure, differing only in syntax and data type handling. The core idea of the sliding window remains the same across all implementations.