- {x}
- Global and Local Inversions
- Split BST
- Swap Adjacent in LR String
- Swim in Rising Water
- K-th Symbol in Grammar
- Reaching Points
- Rabbits in Forest
- Transform to Chessboard
- Minimum Distance Between BST Nodes
- Letter Case Permutation
- Is Graph Bipartite?
- K-th Smallest Prime Fraction
- Cheapest Flights Within K Stops
- Rotated Digits
- Escape The Ghosts
- Domino and Tromino Tiling
- Custom Sort String
- Read More...

Minimum Distance Between BST Nodes
Given the root of a Binary Search Tree (BST), return the minimum difference between the values of any two different nodes in the tree.
Example 1:
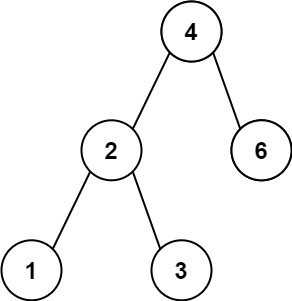
Input: root = [4,2,6,1,3] Output: 1
Example 2:
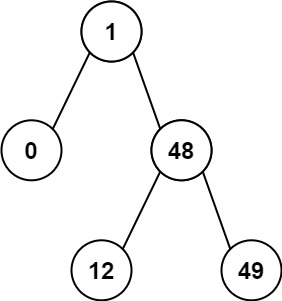
Input: root = [1,0,48,null,null,12,49] Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 100]. 0 <= Node.val <= 105
Note: This question is the same as 530: https://leetcode.com/problems/minimum-absolute-difference-in-bst/
Solution Explanation: Minimum Distance Between BST Nodes
This problem asks to find the minimum difference between the values of any two different nodes in a Binary Search Tree (BST). The key insight is leveraging the property of a BST: an inorder traversal yields a sorted sequence of node values. Therefore, the minimum difference will always exist between two adjacent nodes in this sorted sequence.
Approach: Inorder Traversal
The optimal approach involves performing an inorder traversal of the BST. We keep track of the previously visited node's value (pre). During the traversal, for each node, we calculate the difference between its value and pre. The minimum of these differences is the solution.
Algorithm:
-
Initialization: Set
preto negative infinity (-inf) to handle the first node correctly. Initializeans(the minimum difference) to positive infinity (inf). -
Inorder Traversal (Recursive or Iterative):
- Recursively (or iteratively) traverse the tree in inorder fashion.
- For each node visited:
- Calculate the difference
diff = current_node.val - pre. - Update
ansasans = min(ans, diff). - Update
preto the current node's value (pre = current_node.val).
- Calculate the difference
-
Return
ans: After the traversal,ansholds the minimum difference.
Time and Space Complexity Analysis:
- Time Complexity: O(N), where N is the number of nodes in the BST. This is because we visit each node exactly once during the inorder traversal.
- Space Complexity: O(H) in the recursive approach, where H is the height of the tree (worst case O(N) for a skewed tree). An iterative approach using a stack would have O(H) space complexity as well. In a balanced BST, H would be log(N).
Code Implementation (Python):
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def minDiffInBST(self, root: TreeNode) -> int:
import math
pre = -math.inf # Initialize pre to negative infinity
ans = math.inf # Initialize ans to positive infinity
def inorder(node):
nonlocal pre, ans #Access and modify outer scope vars
if node:
inorder(node.left)
diff = node.val - pre
ans = min(ans, diff)
pre = node.val
inorder(node.right)
inorder(root)
return ansThe code in other languages follows the same logic, differing only in syntax and specific library functions (like Math.min in JavaScript, min in Go, etc.). The core algorithm remains consistent across all implementations.