- {x}
- Basic Calculator IV
- Jewels and Stones
- Basic Calculator III
- Sliding Puzzle
- Minimize Max Distance to Gas Station
- Global and Local Inversions
- Split BST
- Swap Adjacent in LR String
- Swim in Rising Water
- K-th Symbol in Grammar
- Reaching Points
- Rabbits in Forest
- Transform to Chessboard
- Minimum Distance Between BST Nodes
- Letter Case Permutation
- Is Graph Bipartite?
- K-th Smallest Prime Fraction
- Read More...

Swim in Rising Water
You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).
The rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.
Return the least time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).
Example 1:
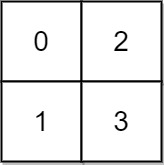
Input: grid = [[0,2],[1,3]] Output: 3 Explanation: At time 0, you are in grid location (0, 0). You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0. You cannot reach point (1, 1) until time 3. When the depth of water is 3, we can swim anywhere inside the grid.
Example 2:
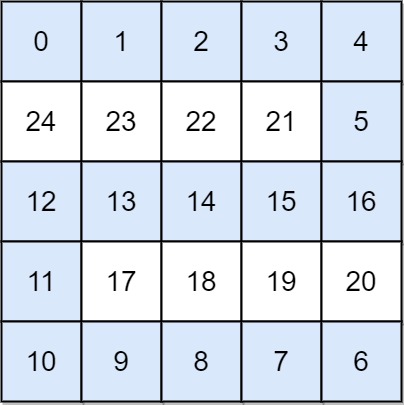
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]] Output: 16 Explanation: The final route is shown. We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 500 <= grid[i][j] < n2- Each value
grid[i][j]is unique.
Solution Explanation:
The problem asks for the minimum time required to reach the bottom-right corner (n-1, n-1) from the top-left corner (0,0) of an n x n grid, given that you can only move to adjacent cells with elevation less than or equal to the current time t. This is essentially a shortest path problem with a time-dependent constraint.
Several approaches can solve this, including binary search and union-find. The provided solutions use a Union-Find approach which is efficient for this problem.
Union-Find Approach:
The core idea is to use a Union-Find data structure to track connected components in the grid at different time steps.
-
Initialization:
- Create a Union-Find data structure
pto represent the connected components. Initially, each cell is its own component. - Create an array
hito map the elevation values to their corresponding cell indices (row * n + col). This allows efficient lookup of cell indices based on elevation.
- Create a Union-Find data structure
-
Iterative Time Steps:
- Iterate through time
tfrom 0 to n*n -1 (maximum possible elevation). - At each time step, process cells with elevation
<= t. - For each cell (i, j) with elevation
<= t:- Check its four neighbors.
- If a neighbor (x, y) also has elevation
<= t, union the components of (i, j) and (x, y) usingfindandunionoperations.
- Iterate through time
-
Check Connectivity:
- After processing all cells with elevation
<= t, check if the top-left (0) and bottom-right (n*n - 1) cells belong to the same component using thefindfunction. - If they are in the same component, it means a path exists from (0,0) to (n-1, n-1) at time
t, so returnt.
- After processing all cells with elevation
-
Return Result:
- If the loop completes without finding a path, it implies there is an error (though this shouldn't happen with the given constraints).
Time Complexity Analysis:
- The outer loop iterates
n*ntimes. - Inside the loop, we iterate through at most
4*n*nneighbors for union operation. - The
findandunionoperations in the Union-Find structure have an amortized time complexity of almost O(1) due to path compression and union by rank (though it could be O(log n) in the worst case without optimizations).
Therefore, the overall time complexity is approximately O(n*n) (dominated by the outer loop and neighbor checks), which is efficient for the given constraints (1 <= n <= 50).
Space Complexity Analysis:
The space complexity is O(n*n) due to the p and hi arrays, which store information about the cells.
Code Explanation (Python3 as Example):
class Solution:
def swimInWater(self, grid: List[List[int]]) -> int:
def find(x): # Find operation for Union-Find
if p[x] != x:
p[x] = find(p[x])
return p[x]
n = len(grid)
p = list(range(n * n)) # Initialize Union-Find
hi = [0] * (n * n) # Mapping elevation to cell index
for i, row in enumerate(grid):
for j, h in enumerate(row):
hi[h] = i * n + j # Store cell index for each elevation
for t in range(n * n): # Iterate through time steps
i, j = divmod(hi[t], n) # Get cell coordinates from index
for a, b in [(0, -1), (0, 1), (1, 0), (-1, 0)]: #Check neighbors
x, y = i + a, j + b
if 0 <= x < n and 0 <= y < n and grid[x][y] <= t:
p[find(x * n + y)] = find(hi[t]) #Union if neighbor is accessible
if find(0) == find(n * n - 1): #Check if connected
return t
return -1 # Should not reach here with given constraints
The other languages (Java, C++, Go, TypeScript, Rust) follow a similar structure, implementing the Union-Find and the iterative time step process. The core logic remains the same across all the languages. The only difference lies in the syntax and standard library functions used.