- {x}
- Maximum Binary Tree
- Print Binary Tree
- Coin Path
- Robot Return to Origin
- Find K Closest Elements
- Split Array into Consecutive Subsequences
- Remove 9
- Image Smoother
- Maximum Width of Binary Tree
- Equal Tree Partition
- Strange Printer
- Non-decreasing Array
- Path Sum IV
- Beautiful Arrangement II
- Kth Smallest Number in Multiplication Table
- Trim a Binary Search Tree
- Maximum Swap
- Read More...

Maximum Width of Binary Tree
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
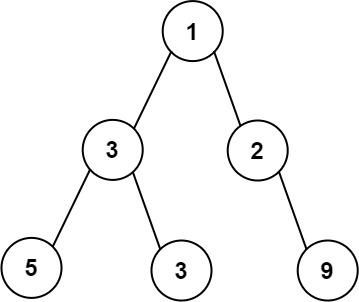
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:
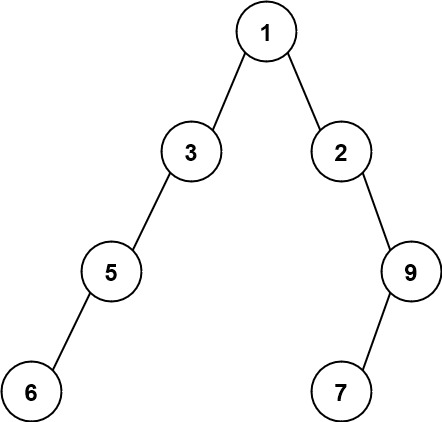
Input: root = [1,3,2,5,null,null,9,6,null,7] Output: 7 Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3:
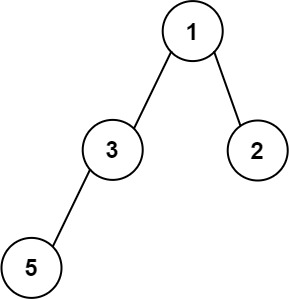
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
662. Maximum Width of Binary Tree
This problem asks to find the maximum width of a binary tree. The width of a level is the length between the leftmost and rightmost non-null nodes, including null nodes between them.
Approach 1: Breadth-First Search (BFS)
This approach uses BFS to traverse the tree level by level. We assign each node a unique index based on its position in the level. The leftmost node at each level gets index 1, the next node gets index 2, and so on. We use a queue to store pairs of (node, index).
Algorithm:
- Initialization: Create a queue
qcontaining the root node with index 1. Initializemax_widthto 0. - Iteration: While the queue is not empty:
- Update
max_widthto the maximum ofmax_widthand the difference between the last node's index and the first node's index plus 1. This represents the width of the current level. - Process nodes in the current level. For each node:
- If the node has a left child, add the left child to the queue with index
2 * index. - If the node has a right child, add the right child to the queue with index
2 * index + 1.
- If the node has a left child, add the left child to the queue with index
- Update
- Return: Return
max_width.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and processed once.
Space Complexity: O(W), where W is the maximum width of the tree. In the worst case (a complete binary tree), W can be proportional to N.
Approach 2: Depth-First Search (DFS)
This approach uses DFS to traverse the tree. It maintains a list t to store the index of the leftmost node at each level.
Algorithm:
- Initialization: Create an empty list
tand setans(maximum width) to 1. - DFS Function: Recursively traverse the tree. For each node:
- If the current depth is not in
t, append the indexitot. - Otherwise, update
ansto the maximum ofansandi - t[depth] + 1. - Recursively call DFS for left and right children with updated index (
i * 2andi * 2 + 1respectively) and depth.
- If the current depth is not in
- Return: Return
ans.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited and processed once.
Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack in the worst case, and the size of t which is at most H.
Code Examples (Python)
Approach 1 (BFS):
from collections import deque
class Solution:
def widthOfBinaryTree(self, root):
if not root:
return 0
q = deque([(root, 1)])
max_width = 0
while q:
max_width = max(max_width, q[-1][1] - q[0][1] + 1)
for _ in range(len(q)):
node, index = q.popleft()
if node.left:
q.append((node.left, index * 2))
if node.right:
q.append((node.right, index * 2 + 1))
return max_width
Approach 2 (DFS):
class Solution:
def widthOfBinaryTree(self, root):
self.ans = 1
self.t = []
self.dfs(root, 0, 1)
return self.ans
def dfs(self, root, depth, i):
if not root:
return
if len(self.t) == depth:
self.t.append(i)
else:
self.ans = max(self.ans, i - self.t[depth] + 1)
self.dfs(root.left, depth + 1, i * 2)
self.dfs(root.right, depth + 1, i * 2 + 1)
Both approaches have the same time complexity, but the BFS approach might be slightly more space-efficient for very wide trees because the DFS approach's space complexity depends on the height of the tree. The BFS approach's space complexity depends on the maximum width of the tree. For balanced trees, both have similar space complexity. For skewed trees, BFS can use significantly less space.