- {x}
- Remove 9
- Image Smoother
- Maximum Width of Binary Tree
- Equal Tree Partition
- Strange Printer
- Non-decreasing Array
- Path Sum IV
- Beautiful Arrangement II
- Kth Smallest Number in Multiplication Table
- Trim a Binary Search Tree
- Maximum Swap
- Second Minimum Node In a Binary Tree
- Bulb Switcher II
- Number of Longest Increasing Subsequence
- Longest Continuous Increasing Subsequence
- Cut Off Trees for Golf Event
- Implement Magic Dictionary
- Read More...

Kth Smallest Number in Multiplication Table
Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).
Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.
Example 1:
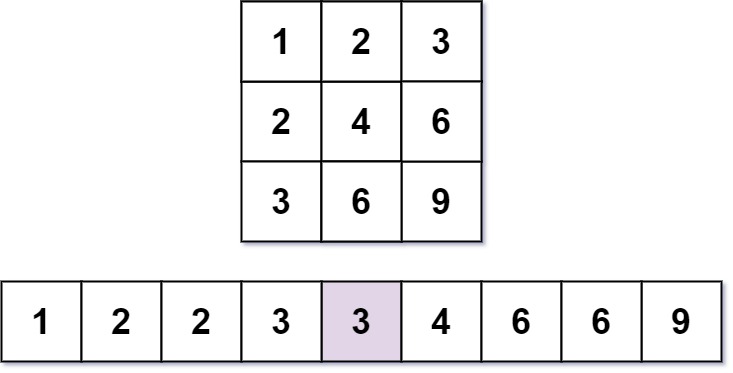
Input: m = 3, n = 3, k = 5 Output: 3 Explanation: The 5th smallest number is 3.
Example 2:
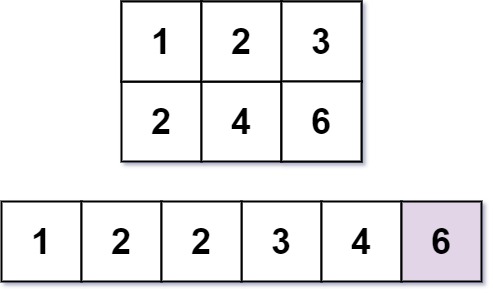
Input: m = 2, n = 3, k = 6 Output: 6 Explanation: The 6th smallest number is 6.
Constraints:
1 <= m, n <= 3 * 1041 <= k <= m * n
Solution Explanation:
This problem asks to find the k-th smallest element in an m x n multiplication table. A brute-force approach of generating the entire table and sorting would be highly inefficient, especially for large m and n. Instead, we can leverage binary search for an optimized solution.
Approach:
The core idea is to use binary search on the range of possible values (1 to m*n). For each potential k-th smallest number ( mid in the code), we count how many numbers in the multiplication table are less than or equal to mid. This count is compared with k.
-
Binary Search: We initialize
leftto 1 andrightto m*n, representing the smallest and largest possible values in the table. The binary search iteratively narrows down the search space. -
Counting Numbers: For a given
mid, we iterate through each row (i) of the multiplication table. For each row, we determine the maximum column index (j) such thati*j <= mid. This is efficiently calculated usingmin(mid/i, n). The total count of numbers less than or equal tomidis accumulated. -
Comparison and Adjustment:
- If the
cnt(count of numbers <=mid) is greater than or equal tok, it means the k-th smallest number is in the lower half of the search space. We updaterighttomidto search in the lower half. - If
cntis less thank, the k-th smallest number lies in the upper half. We updatelefttomid + 1.
- If the
-
Result: The loop continues until
leftequalsright. At this point,left(orright) represents the k-th smallest number in the multiplication table.
Time Complexity: O(m log(m*n))
The binary search takes O(log(mn)) iterations. In each iteration, the inner loop iterates through 'm' rows, performing a constant-time operation (min(mid/i, n)). Thus the dominant factor in the time complexity is m * log(mn).
Space Complexity: O(1)
The algorithm uses a constant amount of extra space to store variables like left, right, mid, and cnt. It doesn't require additional data structures proportional to the input size.
Code Explanation (Python3 Example):
class Solution:
def findKthNumber(self, m: int, n: int, k: int) -> int:
left, right = 1, m * n # Initialize the search space
while left < right: # Binary search loop
mid = (left + right) >> 1 #Efficient way to calculate average
cnt = 0
for i in range(1, m + 1): # Iterate through rows
cnt += min(mid // i, n) # Count numbers <= mid in each row
if cnt >= k: # If count >= k, kth smallest is in lower half
right = mid
else: # Otherwise, in upper half
left = mid + 1
return left # left(or right) is the kth smallest numberThe Java, C++, and Go code implementations follow the same logic and algorithmic steps, differing only in syntax. They all achieve the same time and space complexity.