- {x}
- Palindromic Substrings
- Replace Words
- Dota2 Senate
- 2 Keys Keyboard
- 4 Keys Keyboard
- Find Duplicate Subtrees
- Two Sum IV - Input is a BST
- Maximum Binary Tree
- Print Binary Tree
- Coin Path
- Robot Return to Origin
- Find K Closest Elements
- Split Array into Consecutive Subsequences
- Remove 9
- Image Smoother
- Maximum Width of Binary Tree
- Equal Tree Partition
- Read More...

Print Binary Tree
Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:
- The height of the tree is
heightand the number of rowsmshould be equal toheight + 1. - The number of columns
nshould be equal to2height+1 - 1. - Place the root node in the middle of the top row (more formally, at location
res[0][(n-1)/2]). - For each node that has been placed in the matrix at position
res[r][c], place its left child atres[r+1][c-2height-r-1]and its right child atres[r+1][c+2height-r-1]. - Continue this process until all the nodes in the tree have been placed.
- Any empty cells should contain the empty string
"".
Return the constructed matrix res.
Example 1:
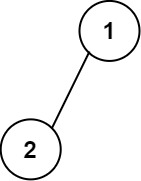
Input: root = [1,2] Output: [["","1",""], ["2","",""]]
Example 2:
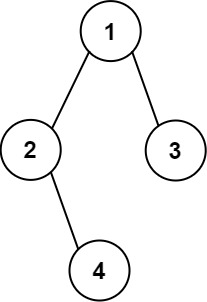
Input: root = [1,2,3,null,4] Output: [["","","","1","","",""], ["","2","","","","3",""], ["","","4","","","",""]]
Constraints:
- The number of nodes in the tree is in the range
[1, 210]. -99 <= Node.val <= 99- The depth of the tree will be in the range
[1, 10].
Solution Explanation for LeetCode 655. Print Binary Tree
This problem asks to create a formatted string matrix representation of a given binary tree. The matrix's dimensions are determined by the tree's height, and node placement follows specific rules based on their position relative to their parent.
Approach
Both solutions employ a Depth-First Search (DFS) and a Breadth-First Search (BFS) approach.
Solution 1 (DFS):
-
Height Calculation: A recursive helper function
height(root)calculates the tree's height. An empty tree has a height of -1; otherwise, it's 1 plus the maximum height of the left and right subtrees. -
Matrix Initialization: A matrix
ansof size (height + 1) x (2height+1 - 1) is created and filled with empty strings. This pre-allocates the space needed to hold the tree representation. -
Depth-First Traversal (dfs): A recursive function
dfs(root, r, c)places nodes into the matrix.- The base case is an empty subtree.
- Otherwise, it places the node's value at the current row
rand columnc. - Recursively calls itself for left and right children, updating the row and column indices according to the problem's rules. The left child is placed at
c - 2<sup>height - r - 1</sup>and the right child atc + 2<sup>height - r - 1</sup>. This formula ensures correct spacing.
Solution 2 (BFS):
-
Height Calculation: A BFS approach is used to calculate the height. A queue is used, traversing level by level to determine the tree's height efficiently.
-
Matrix Initialization: Same as in Solution 1, a matrix of appropriate dimensions is created and filled with empty strings.
-
Breadth-First Traversal: A queue
qis used to store tuples representing(node, row, column). It starts with the root node at the middle of the top row.- It iteratively dequeues tuples, placing the node's value in
ans[r][c]. - Children are enqueued with updated row and column values calculated using the same formula as in Solution 1.
- It iteratively dequeues tuples, placing the node's value in
Time and Space Complexity Analysis
Solution 1 (DFS):
- Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited once during the DFS traversal. The height calculation also takes O(N) in the worst case.
- Space Complexity: O(N) in the worst case (skewed tree) due to the recursive call stack of DFS and the space used to store the result matrix. For a balanced tree, the space complexity would be O(log N) due to the recursive stack's depth, plus O(N) for the matrix, which still would be O(N) overall.
Solution 2 (BFS):
- Time Complexity: O(N). Each node is processed once during the BFS traversal and the height calculation.
- Space Complexity: O(N). The queue in BFS can hold at most all nodes at the widest level (which could be O(N) in a skewed tree). The space used by the result matrix is also O(N).
Code Examples (Python)
Both Python solutions are provided in the original response, showing both DFS and BFS implementations. The choice between DFS and BFS depends on personal preference and the specific characteristics of the input tree. For balanced trees, the difference in performance is usually minimal. For significantly unbalanced trees, BFS might be slightly faster as the depth of the recursion in DFS might grow substantially.