- {x}
- Equal Row and Column Pairs
- Design a Food Rating System
- Number of Excellent Pairs
- Maximum Number of Books You Can Take
- Number of Unique Subjects Taught by Each Teacher
- Make Array Zero by Subtracting Equal Amounts
- Maximum Number of Groups Entering a Competition
- Find Closest Node to Given Two Nodes
- Longest Cycle in a Graph
- Minimum Costs Using the Train Line
- Generate the Invoice
- Merge Similar Items
- Count Number of Bad Pairs
- Task Scheduler II
- Minimum Replacements to Sort the Array
- Number of Arithmetic Triplets
- Reachable Nodes With Restrictions
- Read More...

Longest Cycle in a Graph
You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.
The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.
Return the length of the longest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node.
Example 1:
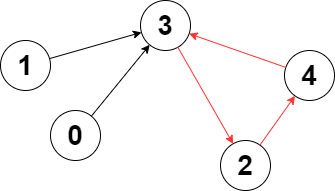
Input: edges = [3,3,4,2,3] Output: 3 Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2. The length of this cycle is 3, so 3 is returned.
Example 2:
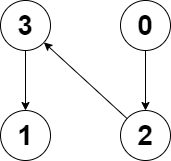
Input: edges = [2,-1,3,1] Output: -1 Explanation: There are no cycles in this graph.
Constraints:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
Solution Explanation: Finding the Longest Cycle in a Directed Graph
This problem involves finding the longest cycle in a directed graph where each node has at most one outgoing edge. The graph is represented as an array edges where edges[i] indicates the node that node i points to. If edges[i] == -1, node i has no outgoing edge.
The solution uses Depth-First Search (DFS) to explore the graph and identify cycles. The key idea is to track visited nodes during the traversal. If we encounter a node that has already been visited in the current path, we've found a cycle.
Algorithm:
-
Initialization: Create a
visitedarray to keep track of visited nodes. Initializeans(the length of the longest cycle) to -1. -
Iterate through nodes: Iterate through each node
iin the graph. -
DFS Traversal: If node
ihasn't been visited:- Start a DFS traversal from node
i. - Maintain a
cyclelist to store the nodes visited during the current path. - Mark each visited node in
visitedastrue. - Continue the traversal until one of the following happens:
- We reach a node with no outgoing edge (
edges[j] == -1). In this case, the current path doesn't contain a cycle, so we move to the next node. - We encounter a node
jthat's already present incycle. This indicates a cycle. We calculate the cycle length ascycle.length - k, wherekis the index of the repeated nodejincycle. We updateanswith the maximum cycle length found so far.
- We reach a node with no outgoing edge (
- Start a DFS traversal from node
-
Return Result: After processing all nodes, return
ans. If no cycle was found,ansremains -1.
Time Complexity Analysis:
The algorithm iterates through each node once (O(n)) and performs a DFS traversal for each unvisited node. In the worst case, the DFS traversal might visit all n nodes. Therefore, the overall time complexity is O(n), since each edge is visited at most once.
Space Complexity Analysis:
The algorithm uses a visited array of size n and a cycle list. In the worst case, the cycle list could contain all n nodes. Therefore, the overall space complexity is O(n).
Code Examples (Python):
class Solution:
def longestCycle(self, edges: List[int]) -> int:
n = len(edges)
visited = [False] * n
ans = -1
def dfs(node, path):
nonlocal ans
visited[node] = True
path.append(node)
next_node = edges[node]
if next_node != -1:
if visited[next_node]:
index = path.index(next_node)
ans = max(ans, len(path) - index)
else:
dfs(next_node, path.copy())
for i in range(n):
if not visited[i]:
dfs(i, [])
return ansThis Python code directly implements the algorithm described above, utilizing recursion for the DFS traversal and keeping track of the current path using a list. The nonlocal keyword allows modifying the ans variable from within the nested function.
The other languages (Java, C++, Go, TypeScript) implement essentially the same algorithm with minor syntactic variations. The core logic of iterative node processing and DFS traversal with cycle detection remains consistent across all implementations.