- {x}
- Minimum Deletions to Make Array Divisible
- Finding the Number of Visible Mountains
- Compute the Rank as a Percentage
- Best Poker Hand
- Number of Zero-Filled Subarrays
- Design a Number Container System
- Shortest Impossible Sequence of Rolls
- First Letter to Appear Twice
- Equal Row and Column Pairs
- Design a Food Rating System
- Number of Excellent Pairs
- Maximum Number of Books You Can Take
- Number of Unique Subjects Taught by Each Teacher
- Make Array Zero by Subtracting Equal Amounts
- Maximum Number of Groups Entering a Competition
- Find Closest Node to Given Two Nodes
- Longest Cycle in a Graph
- Read More...

Equal Row and Column Pairs
Given a 0-indexed n x n integer matrix grid, return the number of pairs (ri, cj) such that row ri and column cj are equal.
A row and column pair is considered equal if they contain the same elements in the same order (i.e., an equal array).
Example 1:
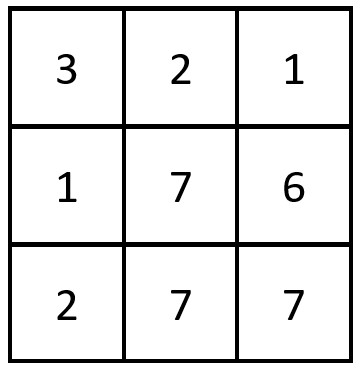
Input: grid = [[3,2,1],[1,7,6],[2,7,7]] Output: 1 Explanation: There is 1 equal row and column pair: - (Row 2, Column 1): [2,7,7]
Example 2:
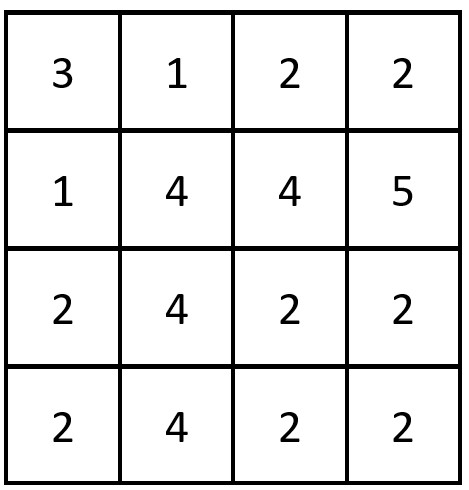
Input: grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]] Output: 3 Explanation: There are 3 equal row and column pairs: - (Row 0, Column 0): [3,1,2,2] - (Row 2, Column 2): [2,4,2,2] - (Row 3, Column 2): [2,4,2,2]
Constraints:
n == grid.length == grid[i].length1 <= n <= 2001 <= grid[i][j] <= 105
Solution Explanation:
The problem asks to find the number of pairs (ri, cj) where row ri and column cj are identical in a given square matrix grid. "Identical" means the elements in the row and column are the same and in the same order.
The solution uses a straightforward simulation approach:
-
Iterate through all possible row-column pairs: The code uses nested loops to iterate through every possible combination of row index
iand column indexjin thegrid. -
Compare row and column: For each pair (i, j), it compares the elements of row
iand columnj. It does this using another inner loop (kloop). If any element in rowidiffers from the corresponding element in columnj, the flagokis set to 0, indicating they are not equal. -
Count equal pairs: If, after checking all elements,
okremains 1, it means rowiand columnjare equal, and theans(answer) counter is incremented. -
Return the count: Finally, the function returns the value of
ans, which represents the total number of equal row-column pairs found.
Time and Space Complexity Analysis
-
Time Complexity: The code has three nested loops, each running up to
ntimes (wherenis the dimension of the square matrix). Therefore, the time complexity is O(n³). This is because for every row-column pair, we need to comparenelements. -
Space Complexity: The algorithm uses only a few variables to store the counters and flags (
ans,ok,i,j,k). The space used is constant regardless of the input size. Thus, the space complexity is O(1).
Code Examples in Different Languages
The code examples provided demonstrate the solution's implementation in Python, Java, C++, Go, and TypeScript. They all follow the same basic logic described above, with minor syntactic differences. The core nested loop structure remains the same across all languages.