- {x}
- First Letter to Appear Twice
- Equal Row and Column Pairs
- Design a Food Rating System
- Number of Excellent Pairs
- Maximum Number of Books You Can Take
- Number of Unique Subjects Taught by Each Teacher
- Make Array Zero by Subtracting Equal Amounts
- Maximum Number of Groups Entering a Competition
- Find Closest Node to Given Two Nodes
- Longest Cycle in a Graph
- Minimum Costs Using the Train Line
- Generate the Invoice
- Merge Similar Items
- Count Number of Bad Pairs
- Task Scheduler II
- Minimum Replacements to Sort the Array
- Number of Arithmetic Triplets
- Read More...

Find Closest Node to Given Two Nodes
You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.
The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from i, then edges[i] == -1.
You are also given two integers node1 and node2.
Return the index of the node that can be reached from both node1 and node2, such that the maximum between the distance from node1 to that node, and from node2 to that node is minimized. If there are multiple answers, return the node with the smallest index, and if no possible answer exists, return -1.
Note that edges may contain cycles.
Example 1:
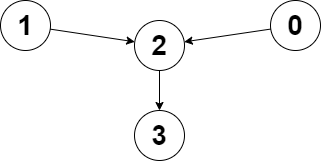
Input: edges = [2,2,3,-1], node1 = 0, node2 = 1 Output: 2 Explanation: The distance from node 0 to node 2 is 1, and the distance from node 1 to node 2 is 1. The maximum of those two distances is 1. It can be proven that we cannot get a node with a smaller maximum distance than 1, so we return node 2.
Example 2:
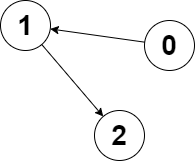
Input: edges = [1,2,-1], node1 = 0, node2 = 2 Output: 2 Explanation: The distance from node 0 to node 2 is 2, and the distance from node 2 to itself is 0. The maximum of those two distances is 2. It can be proven that we cannot get a node with a smaller maximum distance than 2, so we return node 2.
Constraints:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i0 <= node1, node2 < n
Solution Explanation
This problem asks to find the node in a directed graph that is reachable from both node1 and node2, minimizing the maximum distance from either node to the found node.
The solution uses Dijkstra's algorithm to compute the shortest distances from node1 and node2 to all other nodes in the graph. Dijkstra's algorithm is chosen because it efficiently finds the shortest paths in a graph with non-negative edge weights (in this case, the edge weights are implicitly 1).
Algorithm:
-
Graph Representation: The input
edgesarray is transformed into an adjacency list representation of the graph. This allows for efficient traversal of the graph's neighbors. -
Dijkstra's Algorithm (Twice): Dijkstra's algorithm is run twice: once starting from
node1and once fromnode2. This produces two arrays,d1andd2, whered1[i]is the shortest distance fromnode1to nodei, andd2[i]is the shortest distance fromnode2to nodei. If a node is unreachable, its distance will be infinity. -
Finding the Closest Node: The code then iterates through the nodes, comparing
d1[i]andd2[i]. It selects the nodeithat minimizesmax(d1[i], d2[i]). This represents the node with the smallest maximum distance from both starting nodes. The node with the smallest index among those with the minimum maximum distance is selected. -
Handling Unreachable Nodes: The algorithm implicitly handles cases where a node is unreachable from either
node1ornode2. Because Dijkstra's algorithm returns infinity (a large value in the code) for unreachable nodes,max(d1[i], d2[i])will be large for those nodes, ensuring they aren't selected as the closest node. -
Return Value: The function returns the index of the closest node found. If no such node exists (i.e., no node is reachable from both
node1andnode2), it returns-1.
Time Complexity Analysis:
- Dijkstra's algorithm has a time complexity of O(E log V), where E is the number of edges and V is the number of vertices (nodes) in the graph. Since we run Dijkstra's algorithm twice, the overall time complexity is dominated by this step, resulting in O(E log V). In the worst case, E could be up to V2 (a complete graph), thus O(V2 log V). However, the problem states that each node has at most one outgoing edge; in this scenario, E is at most V, leading to a complexity of O(V log V).
- The final iteration to find the closest node takes O(V) time.
Therefore, the overall time complexity is O(V log V), dominated by the two Dijkstra's algorithm executions.
Space Complexity Analysis:
- The adjacency list uses O(V + E) space, which simplifies to O(V) since E ≤ V.
- Dijkstra's algorithm uses O(V) space for the distance array and the priority queue.
- The space to store
d1andd2is O(V).
The overall space complexity is therefore O(V).
The provided code solutions in Python, Java, C++, and Go all implement this algorithm. They differ slightly in the way they manage the priority queue (heap) for Dijkstra's algorithm, but the core approach remains consistent. The TypeScript solution uses a simpler queue instead of a priority queue for Dijkstra's, which is correct given that each node has at most one outgoing edge. In this scenario, the simpler BFS-like approach is as efficient as Dijkstra's algorithm.