- {x}
- Beautiful Arrangement II
- Kth Smallest Number in Multiplication Table
- Trim a Binary Search Tree
- Maximum Swap
- Second Minimum Node In a Binary Tree
- Bulb Switcher II
- Number of Longest Increasing Subsequence
- Longest Continuous Increasing Subsequence
- Cut Off Trees for Golf Event
- Implement Magic Dictionary
- Map Sum Pairs
- Valid Parenthesis String
- 24 Game
- Valid Palindrome II
- Next Closest Time
- Baseball Game
- K Empty Slots
- Read More...

Cut Off Trees for Golf Event
You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an m x n matrix. In this matrix:
0means the cell cannot be walked through.1represents an empty cell that can be walked through.- A number greater than
1represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes 1 (an empty cell).
Starting from the point (0, 0), return the minimum steps you need to walk to cut off all the trees. If you cannot cut off all the trees, return -1.
Note: The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
Example 1:

Input: forest = [[1,2,3],[0,0,4],[7,6,5]] Output: 6 Explanation: Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
Example 2:
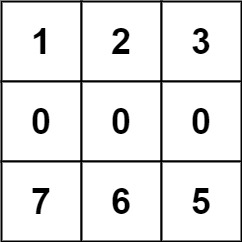
Input: forest = [[1,2,3],[0,0,0],[7,6,5]] Output: -1 Explanation: The trees in the bottom row cannot be accessed as the middle row is blocked.
Example 3:
Input: forest = [[2,3,4],[0,0,5],[8,7,6]] Output: 6 Explanation: You can follow the same path as Example 1 to cut off all the trees. Note that you can cut off the first tree at (0, 0) before making any steps.
Constraints:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109- Heights of all trees are distinct.
Solution Explanation for Cut Off Trees for Golf Event
This problem requires finding the minimum steps to cut off all trees in a forest, starting from (0,0), following the constraint of cutting trees in ascending order of height. The solution uses a combination of sorting and Breadth-First Search (BFS).
1. Data Structures:
- The forest is represented as a 2D array (matrix).
- A priority queue (or min-heap) is used to efficiently manage trees based on their height, ensuring we process them in ascending order. This is crucial for the solution's correctness.
- A hash set (or similar data structure to check for visited nodes during BFS) optimizes the BFS process.
2. Algorithm:
-
Step 1: Extract and Sort Trees: First, we identify all trees (cells with values > 1) in the forest and store them as
(height, row, col)tuples. These tuples are then sorted in ascending order based on the tree heights. This step guarantees we process trees from shortest to tallest. -
Step 2: Iterative BFS: The core of the solution involves iterating through the sorted list of trees. For each tree:
- We perform a BFS starting from the current position (initially (0,0), then the last tree's position).
- The BFS explores adjacent cells, avoiding obstacles (cells with value 0).
- If the target tree is reachable, the BFS returns the minimum steps needed to reach it.
- If the target tree is unreachable (-1 returned from BFS), it indicates we can't cut off all the trees, so we return -1.
- The total number of steps is accumulated.
-
Step 3: Return Total Steps: Finally, the total number of steps calculated from the BFS traversals is returned.
3. Code Implementation (Python):
import heapq
class Solution:
def cutOffTree(self, forest: List[List[int]]) -> int:
m, n = len(forest), len(forest[0])
trees = [(forest[i][j], i, j) for i in range(m) for j in range(n) if forest[i][j] > 1]
trees.sort()
def bfs(i1, j1, i2, j2):
q = [(0, i1, j1)] # (steps, row, col)
visited = set()
while q:
steps, row, col = heapq.heappop(q)
if (row, col) == (i2, j2):
return steps
visited.add((row, col))
for dr, dc in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
nr, nc = row + dr, col + dc
if 0 <= nr < m and 0 <= nc < n and forest[nr][nc] > 0 and (nr, nc) not in visited:
heapq.heappush(q, (steps + 1, nr, nc))
return -1
total_steps = 0
curr_row, curr_col = 0, 0
for _, row, col in trees:
steps = bfs(curr_row, curr_col, row, col)
if steps == -1:
return -1
total_steps += steps
curr_row, curr_col = row, col
return total_steps
4. Time Complexity Analysis:
- Sorting the trees takes O(K log K) time, where K is the number of trees.
- BFS in the worst case visits all cells in the forest, resulting in O(M*N) time complexity for each BFS call. Since we do at most K BFS calls, the overall time complexity becomes O(K * M * N).
5. Space Complexity Analysis:
- Storing the trees takes O(K) space.
- The visited set in BFS takes O(M * N) space in the worst case.
- The queue in BFS also takes O(M * N) space in the worst case.
- Therefore, the total space complexity is O(K + M * N).
In summary, the solution efficiently finds the minimum steps to cut all trees by cleverly combining sorting to ensure order and BFS to find shortest paths, achieving a reasonable time and space complexity for the given constraints. The provided code demonstrates the algorithm effectively in Python, and equivalent implementations can be easily adapted to other programming languages.