- {x}
- Shuffle the Array
- The k Strongest Values in an Array
- Design Browser History
- Paint House III
- Delete N Nodes After M Nodes of a Linked List
- Final Prices With a Special Discount in a Shop
- Subrectangle Queries
- Find Two Non-overlapping Sub-arrays Each With Target Sum
- Allocate Mailboxes
- Sales by Day of the Week
- Running Sum of 1d Array
- Least Number of Unique Integers after K Removals
- Minimum Number of Days to Make m Bouquets
- Kth Ancestor of a Tree Node
- Group Sold Products By The Date
- Clone Binary Tree With Random Pointer
- XOR Operation in an Array
- Read More...

Allocate Mailboxes
Given the array houses where houses[i] is the location of the ith house along a street and an integer k, allocate k mailboxes in the street.
Return the minimum total distance between each house and its nearest mailbox.
The test cases are generated so that the answer fits in a 32-bit integer.
Example 1:
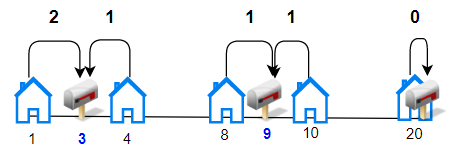
Input: houses = [1,4,8,10,20], k = 3 Output: 5 Explanation: Allocate mailboxes in position 3, 9 and 20. Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5
Example 2:
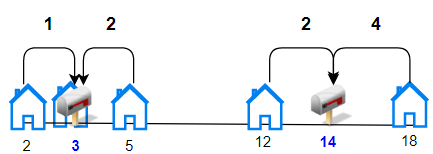
Input: houses = [2,3,5,12,18], k = 2 Output: 9 Explanation: Allocate mailboxes in position 3 and 14. Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.
Constraints:
1 <= k <= houses.length <= 1001 <= houses[i] <= 104- All the integers of
housesare unique.
Solution Explanation:
This problem asks to find the minimum total distance between houses and their nearest mailboxes, given a number of mailboxes k. The solution uses dynamic programming.
Core Idea:
The solution leverages dynamic programming to build up the minimum distance for placing j mailboxes among the first i houses. The state transitions consider all possible positions for the j-th mailbox.
1. Preprocessing:
- The
housesarray is sorted to facilitate calculations. - A 2D array
gis created to store the sum of distances for a contiguous subarray.g[i][j]stores the total distance if mailboxes are placed between housesiandj(inclusive) at the median position. This is calculated efficiently using a cumulative approach.
2. Dynamic Programming:
- A 2D array
fis created, wheref[i][j]represents the minimum total distance to placejmailboxes among the firsti + 1houses. - The base case is
f[i][1] = g[0][i]for eachi, meaning placing one mailbox optimally among the firsti + 1houses. - For
j > 1, the solution iterates through all possible positions (p) for the(j-1)th mailbox. The minimum total distance is the minimum off[p][j-1] + g[p+1][i], representing the minimum cost to placej-1mailboxes among the firstp + 1houses plus the cost to place thejth mailbox among housesp+1toi.
3. Result:
- The final result is
f[n-1][k], representing the minimum total distance when placingkmailboxes among allnhouses.
Time Complexity Analysis:
The dominant part is the nested loops in the DP calculation. The outer loops iterate O(n*k) times, while the inner loop iterates at most O(n) times. This results in a time complexity of O(n²k).
Space Complexity Analysis:
The solution uses two n x n matrices (g) and n x k matrix (f). Thus the space complexity is O(n² + nk). Since k is usually much smaller than n, this can be approximated as O(n²).
Code Explanation (Python):
class Solution:
def minDistance(self, houses: List[int], k: int) -> int:
houses.sort()
n = len(houses)
g = [[0] * n for _ in range(n)] # Precompute cumulative distances
for i in range(n - 2, -1, -1):
for j in range(i + 1, n):
g[i][j] = g[i + 1][j - 1] + houses[j] - houses[i] #Efficiently calculate distances
f = [[float('inf')] * (k + 1) for _ in range(n)] #DP Table
for i in range(n):
f[i][1] = g[0][i] #Base case: 1 mailbox
for j in range(2, min(k + 1, i + 2)): #Iterate through mailbox numbers and house positions
for p in range(i): #Iterate through possible placements of previous mailbox
f[i][j] = min(f[i][j], f[p][j - 1] + g[p + 1][i]) #DP Transition
return f[-1][k] #Final Result
The code in other languages (Java, C++, Go) follows the same logic and algorithmic structure, differing only in syntax and data structure implementations. The core dynamic programming approach remains consistent across all versions.