- {x}
- Minimum Absolute Difference Queries
- Count Salary Categories
- Game of Nim
- Remove One Element to Make the Array Strictly Increasing
- Remove All Occurrences of a Substring
- Maximum Alternating Subsequence Sum
- Design Movie Rental System
- Maximum Product Difference Between Two Pairs
- Cyclically Rotating a Grid
- Number of Wonderful Substrings
- Count Ways to Build Rooms in an Ant Colony
- Leetcodify Friends Recommendations
- Kth Smallest Subarray Sum
- Leetcodify Similar Friends
- Build Array from Permutation
- Eliminate Maximum Number of Monsters
- Count Good Numbers
- Read More...

Cyclically Rotating a Grid
You are given an m x n integer matrix grid, where m and n are both even integers, and an integer k.
The matrix is composed of several layers, which is shown in the below image, where each color is its own layer:
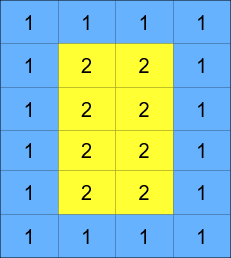
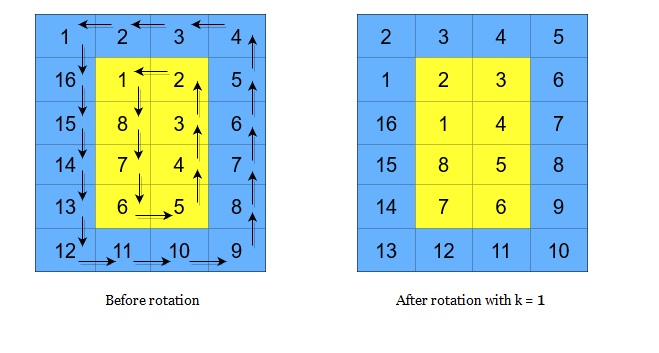
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:
Return the matrix after applying k cyclic rotations to it.
Example 1:
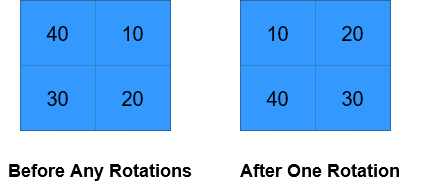
Input: grid = [[40,10],[30,20]], k = 1 Output: [[10,20],[40,30]] Explanation: The figures above represent the grid at every state.
Example 2:
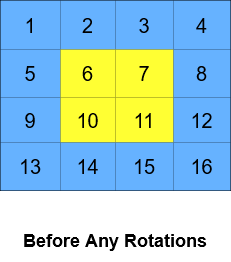
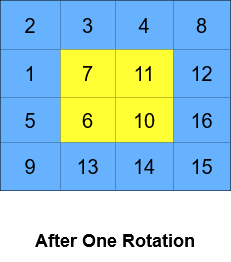
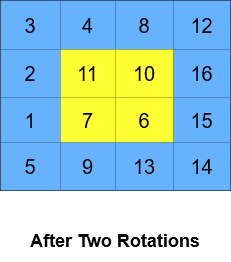
Input: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2 Output: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]] Explanation: The figures above represent the grid at every state.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 50- Both
mandnare even integers. 1 <= grid[i][j] <= 50001 <= k <= 109
Solution Explanation for Cyclically Rotating a Grid
This problem involves cyclically rotating layers of a given matrix. The solution iterates through each layer, extracts its elements, performs a cyclic rotation on those elements, and then places them back into the matrix.
Approach
The core idea is to process the matrix layer by layer. Each layer can be considered a ring. We extract the elements of each ring, rotate them by k positions, and put them back. This rotation is done counter-clockwise. To handle large values of k, we use the modulo operator (%) to ensure that the rotation doesn't exceed the ring's length.
-
Layer Iteration: The solution uses nested loops to iterate through layers. The outer loop iterates from
p = 0tomin(m, n) / 2, wheremandnare the dimensions of the matrix. This represents the layer index, starting from the outermost layer. -
Ring Extraction: For each layer
p, the elements of the ring are extracted into a temporary list or array (nums). This is done by traversing the ring counter-clockwise. -
Cyclic Rotation: The
numslist is rotated bykpositions using list slicing in Python or array manipulation in other languages. The modulo operator (k % len(nums)) handles cases wherekis larger than the ring's length. -
Ring Placement: The rotated elements from
numsare placed back into the matrix in their new positions, again traversing the ring counter-clockwise.
Code Explanation (Python)
class Solution:
def rotateGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
def rotate(p: int, k: int): # Inner function to rotate a single layer
nums = []
# Extract elements from the layer (counter-clockwise)
for j in range(p, n - p - 1):
nums.append(grid[p][j])
for i in range(p, m - p - 1):
nums.append(grid[i][n - p - 1])
for j in range(n - p - 1, p, -1):
nums.append(grid[m - p - 1][j])
for i in range(m - p - 1, p, -1):
nums.append(grid[i][p])
k %= len(nums) # Handle k larger than ring length
nums = nums[k:] + nums[:k] # Perform cyclic rotation
# Place rotated elements back into the grid
idx = 0
for j in range(p, n - p - 1):
grid[p][j] = nums[idx]
idx += 1
for i in range(p, m - p - 1):
grid[i][n - p - 1] = nums[idx]
idx += 1
for j in range(n - p - 1, p, -1):
grid[m - p - 1][j] = nums[idx]
idx += 1
for i in range(m - p - 1, p, -1):
grid[i][p] = nums[idx]
idx += 1
m, n = len(grid), len(grid[0])
for p in range(min(m, n) >> 1): # Iterate through layers
rotate(p, k)
return gridThe other languages (Java, C++, Go, TypeScript) follow a very similar structure, adapting the syntax and data structures to their respective languages.
Time and Space Complexity
-
Time Complexity: O(mn), where
mandnare the dimensions of the matrix. This is because we iterate through each element of the matrix at least once during the extraction and placement phases. The rotation within a layer is O(l), wherelis the layer's perimeter length, and the sum of all layer perimeters is proportional to mn. -
Space Complexity: O(min(m, n)), in the worst case. This is the space used by the temporary array (
nums) to store the elements of a single layer. The space used is proportional to the length of the largest layer's perimeter, which is at most2 * (m + n - 2)(approximately2 * max(m,n)), hence O(min(m, n)). In-place rotation algorithms could reduce this to O(1), but they are more complex to implement.