- {x}
- Path Crossing
- Check If Array Pairs Are Divisible by k
- Number of Subsequences That Satisfy the Given Sum Condition
- Max Value of Equation
- Design a File Sharing System
- Countries You Can Safely Invest In
- Can Make Arithmetic Progression From Sequence
- Last Moment Before All Ants Fall Out of a Plank
- Count Submatrices With All Ones
- Minimum Possible Integer After at Most K Adjacent Swaps On Digits
- Find Root of N-Ary Tree
- Reformat Date
- Range Sum of Sorted Subarray Sums
- Minimum Difference Between Largest and Smallest Value in Three Moves
- Stone Game IV
- Customer Order Frequency
- Number of Good Pairs
- Read More...

Count Submatrices With All Ones
Given an m x n binary matrix mat, return the number of submatrices that have all ones.
Example 1:
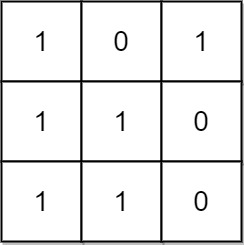
Input: mat = [[1,0,1],[1,1,0],[1,1,0]] Output: 13 Explanation: There are 6 rectangles of side 1x1. There are 2 rectangles of side 1x2. There are 3 rectangles of side 2x1. There is 1 rectangle of side 2x2. There is 1 rectangle of side 3x1. Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.
Example 2:
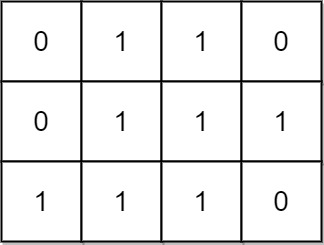
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] Output: 24 Explanation: There are 8 rectangles of side 1x1. There are 5 rectangles of side 1x2. There are 2 rectangles of side 1x3. There are 4 rectangles of side 2x1. There are 2 rectangles of side 2x2. There are 2 rectangles of side 3x1. There is 1 rectangle of side 3x2. Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.
Constraints:
1 <= m, n <= 150mat[i][j]is either0or1.
Solution Explanation: Counting Submatrices with All Ones
This problem asks to count the number of submatrices within a given binary matrix that contain only ones. The optimal solution leverages a combination of prefix sum calculation and iterative counting.
Approach
-
Prefix Sum Calculation: We first preprocess the input matrix
matto create a new matrixg.g[i][j]stores the width of the largest submatrix containing only ones that ends at position (i, j). This is essentially a horizontal prefix sum. Ifmat[i][j]is 0,g[i][j]is 0; otherwise, it's 1 plus the value to its left (g[i][j-1]). -
Iterative Counting: We iterate through each cell (i, j) in the matrix
g. For each cell, we consider it as the bottom-right corner of potential submatrices. We iterate upwards from rowito row 0. For each rowk, we find the minimum width among all the cells in columnjfrom rowkto rowi. This minimum width represents the width of the submatrix with (i,j) as its bottom-right corner and spanning from rowktoi. We add this width to the final count (ans).
Time and Space Complexity Analysis
-
Time Complexity: The preprocessing step (creating
g) takes O(mn) time, where 'm' is the number of rows and 'n' is the number of columns. The nested loops for counting submatrices also take O(mn*m) time in the worst case (innermost loop iterates up to 'm' rows). Therefore, the overall time complexity is O(m²n). -
Space Complexity: We use an auxiliary matrix
gof size mn, resulting in a space complexity of **O(mn)**.
Code Implementation (Python)
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
g = [[0] * n for _ in range(m)] #Initialize the prefix sum matrix
for i in range(m):
for j in range(n):
if mat[i][j]:
g[i][j] = 1 if j == 0 else 1 + g[i][j - 1] #Calculate prefix sum
ans = 0
for i in range(m):
for j in range(n):
col = float('inf') #Initialize minimum column width
for k in range(i, -1, -1):
col = min(col, g[k][j]) #Find minimum width
ans += col #Add to count
return ans
The implementations in other languages (Java, C++, Go, TypeScript) follow the same logic, only differing in syntax and data structure handling. They all achieve the same time and space complexity as the Python solution.