{x}
blog image

Minimum Possible Integer After at Most K Adjacent Swaps On Digits

You are given a string num representing the digits of a very large integer and an integer k. You are allowed to swap any two adjacent digits of the integer at most k times.

Return the minimum integer you can obtain also as a string.

 

Example 1:

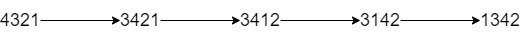
Input: num = "4321", k = 4
Output: "1342"
Explanation: The steps to obtain the minimum integer from 4321 with 4 adjacent swaps are shown.

Example 2:

Input: num = "100", k = 1
Output: "010"
Explanation: It's ok for the output to have leading zeros, but the input is guaranteed not to have any leading zeros.

Example 3:

Input: num = "36789", k = 1000
Output: "36789"
Explanation: We can keep the number without any swaps.

 

Constraints:

  • 1 <= num.length <= 3 * 104
  • num consists of only digits and does not contain leading zeros.
  • 1 <= k <= 109

Solution Explanation

This problem asks to find the lexicographically smallest integer that can be obtained by performing at most k adjacent swaps on the digits of the input number. The solution uses a Binary Indexed Tree (BIT) to efficiently track the cumulative swaps and a greedy approach to select the smallest available digits.

Algorithm:

  1. Initialization:

    • Create a BinaryIndexedTree (BIT) of size n (length of the input number) to track the number of swaps performed on each position. The BIT allows for efficient querying of the cumulative sum of swaps up to a given index and updating the sum at an index in O(log n) time.
    • Create a list or deque (pos) to store the indices of each digit (0-9) in the input number. This helps to quickly find the positions of the available digits.

  2. Greedy Selection:

    • Iterate through each position i (1 to n) of the output string.
    • For each position, iterate through the digits from 0 to 9.
    • For each digit v:
      • Check if the digit exists (i.e., if the pos[v] list is not empty).
      • Calculate the distance dist to swap the smallest available digit v to the current position i. This distance is calculated using the BIT:
        • tree.query(n) - tree.query(j): Gets the total number of swaps performed before position j.
        • j - i: Accounts for the additional swaps required to move digit v from position j to position i.
      • If dist <= k: Sufficient swaps remaining.
        • Update k by subtracting dist.
        • Remove the digit's index j from pos[v].
        • Append the digit v to the output string.
        • Update the BIT with tree.update(j, 1) to reflect that a swap has been performed at position j.
        • Break the inner loop since we've found the digit for the current position.

  3. Return Result: Return the constructed output string.

Time Complexity: O(10n log n). The outer loop iterates n times. The inner loop iterates 10 times (for each digit). BIT operations (query and update) take O(log n) time.

Space Complexity: O(n). The BIT and the pos list use linear space.

Code Explanation (Python):

The Python code implements the above algorithm using a BinaryIndexedTree class. The minInteger function performs the greedy selection and uses a defaultdict(deque) to efficiently manage the indices of each digit. The deque is chosen for efficient removal of the first element.

Code Explanation (Java, C++, Go):

The Java, C++, and Go code provide similar implementations, with the main differences being in syntax and data structures. They all follow the same algorithmic approach using a BinaryIndexedTree and a greedy strategy. The choice of data structure (e.g., ArrayDeque in Java, queue<int> in C++, and a slice in Go) for managing digit indices is tailored to the respective language.

This solution efficiently finds the minimum integer possible within the constraints of at most k adjacent swaps. The use of a Binary Indexed Tree is crucial for optimizing the computation of the total number of swaps required for each digit placement.