- {x}
- Number of Laser Beams in a Bank
- Destroying Asteroids
- Maximum Employees to Be Invited to a Meeting
- Remove All Ones With Row and Column Flips
- Capitalize the Title
- Maximum Twin Sum of a Linked List
- Longest Palindrome by Concatenating Two Letter Words
- Stamping the Grid
- Check if Every Row and Column Contains All Numbers
- Minimum Swaps to Group All 1's Together II
- Count Words Obtained After Adding a Letter
- Earliest Possible Day of Full Bloom
- Pour Water Between Buckets to Make Water Levels Equal
- Divide a String Into Groups of Size k
- Minimum Moves to Reach Target Score
- Solving Questions With Brainpower
- Maximum Running Time of N Computers
- Read More...

Check if Every Row and Column Contains All Numbers
An n x n matrix is valid if every row and every column contains all the integers from 1 to n (inclusive).
Given an n x n integer matrix matrix, return true if the matrix is valid. Otherwise, return false.
Example 1:
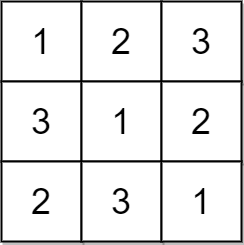
Input: matrix = [[1,2,3],[3,1,2],[2,3,1]] Output: true Explanation: In this case, n = 3, and every row and column contains the numbers 1, 2, and 3. Hence, we return true.
Example 2:
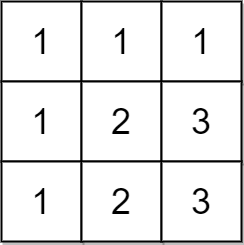
Input: matrix = [[1,1,1],[1,2,3],[1,2,3]] Output: false Explanation: In this case, n = 3, but the first row and the first column do not contain the numbers 2 or 3. Hence, we return false.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 1001 <= matrix[i][j] <= n
Solution Explanation: Check if Every Row and Column Contains All Numbers
This problem asks us to determine if an n x n matrix is valid, meaning every row and every column contains all integers from 1 to n (inclusive). We can solve this efficiently using a hash table (or set in Python) approach.
Approach:
The core idea is to check each row and each column independently to see if they contain all numbers from 1 to n without duplicates. We can achieve this using a hash table (or set) to track the occurrence of each number.
-
Row Check: Iterate through each row of the matrix. For each row:
- Initialize an empty hash table (or set).
- Iterate through the elements of the row.
- For each element, check if it's already in the hash table. If it is, the row is invalid (duplicate found), and we return
false. - If not, add the element to the hash table.
- After processing all elements of the row, check if the size of the hash table equals
n. If not, the row is invalid (missing numbers), and we returnfalse.
-
Column Check: Similarly, iterate through each column of the matrix. For each column:
- Initialize an empty hash table (or set).
- Iterate through the elements of the column (accessing them using
matrix[i][j]wherejis fixed for the column). - Perform the same checks as in the row check: Check for duplicates and ensure all numbers from 1 to
nare present.
-
Return
true: If both the row and column checks pass without returningfalse, it means the matrix is valid, so we returntrue.
Time Complexity: We iterate through each element of the matrix twice (once for rows, once for columns). Therefore, the time complexity is O(n²), where n is the size of the matrix.
Space Complexity: The space complexity is O(n) because, in the worst case, we use a hash table (or set) of size n to store the numbers in a row or column.
Code Implementation (Python):
from itertools import chain
class Solution:
def checkValid(self, matrix: List[List[int]]) -> bool:
n = len(matrix)
return all(len(set(row)) == n for row in chain(matrix, zip(*matrix)))This Python solution elegantly uses itertools.chain to combine rows and columns and set to efficiently check for duplicates and the presence of all numbers 1 to n. zip(*matrix) transposes the matrix, effectively providing the columns as iterables.
Code Implementation (Java, C++, Go, TypeScript):
The Java, C++, Go, and TypeScript solutions follow a similar structure to the Python solution described in the Approach section. They explicitly iterate through rows and columns, using boolean arrays (vis) to track seen numbers.
Example (Java):
class Solution {
public boolean checkValid(int[][] matrix) {
int n = matrix.length;
boolean[] vis = new boolean[n + 1]; //boolean array for efficient duplicate check
//Row Check
for (int[] row : matrix) {
Arrays.fill(vis, false); //Reset for each row
for (int x : row) {
if (vis[x]) return false; //Duplicate found
vis[x] = true;
}
for(int i=1; i<=n; ++i){
if(!vis[i]) return false; //Missing number
}
}
//Column Check
for (int j = 0; j < n; ++j) {
Arrays.fill(vis, false); //Reset for each column
for (int i = 0; i < n; ++i) {
int x = matrix[i][j];
if (vis[x]) return false; //Duplicate found
vis[x] = true;
}
for(int i=1; i<=n; ++i){
if(!vis[i]) return false; //Missing number
}
}
return true;
}
}The other language implementations are structurally similar, using their respective data structures for efficient duplicate detection. The key is the two-pass approach (rows, then columns) and the use of a hash table or boolean array for efficient lookup.