{x}
blog image

Earliest Possible Day of Full Bloom

You have n flower seeds. Every seed must be planted first before it can begin to grow, then bloom. Planting a seed takes time and so does the growth of a seed. You are given two 0-indexed integer arrays plantTime and growTime, of length n each:

  • plantTime[i] is the number of full days it takes you to plant the ith seed. Every day, you can work on planting exactly one seed. You do not have to work on planting the same seed on consecutive days, but the planting of a seed is not complete until you have worked plantTime[i] days on planting it in total.
  • growTime[i] is the number of full days it takes the ith seed to grow after being completely planted. After the last day of its growth, the flower blooms and stays bloomed forever.

From the beginning of day 0, you can plant the seeds in any order.

Return the earliest possible day where all seeds are blooming.

 

Example 1:

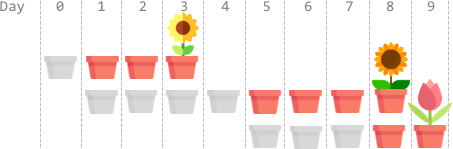
Input: plantTime = [1,4,3], growTime = [2,3,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 0, plant the 0th seed. The seed grows for 2 full days and blooms on day 3.
On days 1, 2, 3, and 4, plant the 1st seed. The seed grows for 3 full days and blooms on day 8.
On days 5, 6, and 7, plant the 2nd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 2:

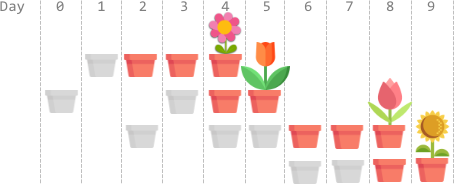
Input: plantTime = [1,2,3,2], growTime = [2,1,2,1]
Output: 9
Explanation: The grayed out pots represent planting days, colored pots represent growing days, and the flower represents the day it blooms.
One optimal way is:
On day 1, plant the 0th seed. The seed grows for 2 full days and blooms on day 4.
On days 0 and 3, plant the 1st seed. The seed grows for 1 full day and blooms on day 5.
On days 2, 4, and 5, plant the 2nd seed. The seed grows for 2 full days and blooms on day 8.
On days 6 and 7, plant the 3rd seed. The seed grows for 1 full day and blooms on day 9.
Thus, on day 9, all the seeds are blooming.

Example 3:

Input: plantTime = [1], growTime = [1]
Output: 2
Explanation: On day 0, plant the 0th seed. The seed grows for 1 full day and blooms on day 2.
Thus, on day 2, all the seeds are blooming.

 

Constraints:

  • n == plantTime.length == growTime.length
  • 1 <= n <= 105
  • 1 <= plantTime[i], growTime[i] <= 104

Solution Explanation: Earliest Possible Day of Full Bloom

This problem asks to find the earliest day when all flowers bloom, given planting and growing times for each seed. A greedy approach coupled with sorting provides an optimal solution.

Intuition:

The total time to plant all seeds is fixed, regardless of order. The key is to minimize the overall blooming time. This can be achieved by prioritizing seeds with longer growing times. By planting those seeds first, we ensure they have sufficient time to bloom before the later ones are even fully planted.

Algorithm:

  1. Sort: Create pairs of (plantTime[i], growTime[i]) for each seed. Sort these pairs in descending order based on growTime. This prioritizes seeds with longer growing times.

  2. Iterate and Accumulate: Initialize totalPlantingTime to 0 and maxBloomDay to 0. Iterate through the sorted pairs. For each seed:

    • Add its plantTime to totalPlantingTime. This represents the total time spent planting up to this seed.
    • Calculate the bloom day for this seed: totalPlantingTime + growTime.
    • Update maxBloomDay to be the maximum of the current maxBloomDay and the bloom day of this seed.

  3. Return: The maxBloomDay after iterating through all seeds represents the earliest day when all flowers bloom.

Time Complexity: O(n log n) due to sorting the pairs. The iteration takes linear time.

Space Complexity: O(n) to store the pairs, though in-place sorting could reduce space usage in some languages.

Code Examples (Python):

class Solution:
    def earliestFullBloom(self, plantTime: List[int], growTime: List[int]) -> int:
        n = len(plantTime)
        seeds = sorted(zip(plantTime, growTime), key=lambda x: -x[1])  #Sort by growTime descending
        total_planting_time = 0
        max_bloom_day = 0
        for plant, grow in seeds:
            total_planting_time += plant
            max_bloom_day = max(max_bloom_day, total_planting_time + grow)
        return max_bloom_day

Other Languages: The core logic remains the same across different programming languages. The primary difference lies in the syntax for sorting and handling pairs (tuples, arrays, etc.). The provided solution in the original response demonstrates this with Java, C++, Go, TypeScript, and Rust. The approaches are functionally equivalent to the Python example above.