- {x}
- Abbreviating the Product of a Range
- Build the Equation
- A Number After a Double Reversal
- Execution of All Suffix Instructions Staying in a Grid
- Intervals Between Identical Elements
- Recover the Original Array
- Minimum Operations to Remove Adjacent Ones in Matrix
- Check if All A's Appears Before All B's
- Number of Laser Beams in a Bank
- Destroying Asteroids
- Maximum Employees to Be Invited to a Meeting
- Remove All Ones With Row and Column Flips
- Capitalize the Title
- Maximum Twin Sum of a Linked List
- Longest Palindrome by Concatenating Two Letter Words
- Stamping the Grid
- Check if Every Row and Column Contains All Numbers
- Read More...

Number of Laser Beams in a Bank
Anti-theft security devices are activated inside a bank. You are given a 0-indexed binary string array bank representing the floor plan of the bank, which is an m x n 2D matrix. bank[i] represents the ith row, consisting of '0's and '1's. '0' means the cell is empty, while'1' means the cell has a security device.
There is one laser beam between any two security devices if both conditions are met:
- The two devices are located on two different rows:
r1andr2, wherer1 < r2. - For each row
iwherer1 < i < r2, there are no security devices in theithrow.
Laser beams are independent, i.e., one beam does not interfere nor join with another.
Return the total number of laser beams in the bank.
Example 1:
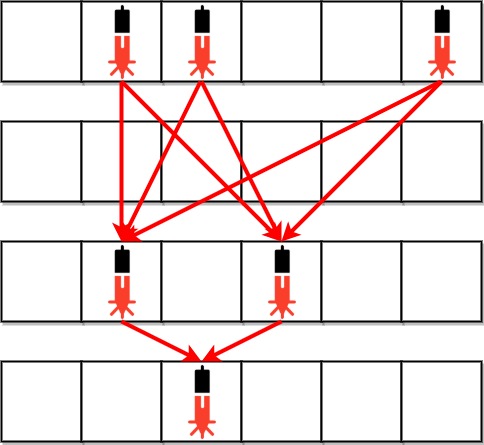
Input: bank = ["011001","000000","010100","001000"] Output: 8 Explanation: Between each of the following device pairs, there is one beam. In total, there are 8 beams: * bank[0][1] -- bank[2][1] * bank[0][1] -- bank[2][3] * bank[0][2] -- bank[2][1] * bank[0][2] -- bank[2][3] * bank[0][5] -- bank[2][1] * bank[0][5] -- bank[2][3] * bank[2][1] -- bank[3][2] * bank[2][3] -- bank[3][2] Note that there is no beam between any device on the 0th row with any on the 3rd row. This is because the 2nd row contains security devices, which breaks the second condition.
Example 2:
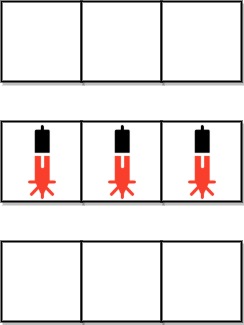
Input: bank = ["000","111","000"] Output: 0 Explanation: There does not exist two devices located on two different rows.
Constraints:
m == bank.lengthn == bank[i].length1 <= m, n <= 500bank[i][j]is either'0'or'1'.
Solution Explanation for Number of Laser Beams in a Bank
This problem asks us to count the number of laser beams formed between security devices in a bank represented by a binary string array. A laser beam exists between two devices if they are on different rows, and no other devices are present in the rows between them.
Approach: Iterative Counting
The most efficient approach is to iterate through the rows of the bank and count the number of security devices (1s) in each row. We maintain a variable pre to store the count from the previous row. For each row with security devices:
- Calculate the current count: Count the number of
1s in the current row (cur). - Calculate beam contribution: If
curis greater than 0 (meaning there are devices in the current row), multiplycurbypre(the number of devices in the previous row). This gives us the number of beams formed between the current and previous row. Add this to the total beam count (ans). - Update
pre: Updateprewithcurfor the next iteration.
This approach avoids nested loops, resulting in a significantly faster solution than checking all pairs of devices.
Time and Space Complexity Analysis
-
Time Complexity: O(m*n), where 'm' is the number of rows and 'n' is the number of columns in the input array. This is because we iterate through each row and count the
1s in each row. The counting operation within each row takes at most O(n) time. -
Space Complexity: O(1). We only use a few integer variables to store the counts and the total number of beams, which uses constant extra space regardless of the input size.
Code Implementation in Multiple Languages
The code implementations below showcase this approach in several popular programming languages. Note that slight variations may exist due to language-specific features, but the core logic remains the same.
Python3
class Solution:
def numberOfBeams(self, bank: List[str]) -> int:
ans = pre = 0
for row in bank:
cur = row.count('1') # Efficiently counts '1's in a row
if cur:
ans += pre * cur
pre = cur
return ans
Java
class Solution {
public int numberOfBeams(String[] bank) {
int ans = 0, pre = 0;
for (String row : bank) {
int cur = 0;
for (char c : row.toCharArray()) {
if (c == '1') cur++;
}
if (cur > 0) {
ans += pre * cur;
pre = cur;
}
}
return ans;
}
}C++
class Solution {
public:
int numberOfBeams(vector<string>& bank) {
int ans = 0, pre = 0;
for (const string& row : bank) {
int cur = count(row.begin(), row.end(), '1'); // Efficient count using STL algorithm
if (cur > 0) {
ans += pre * cur;
pre = cur;
}
}
return ans;
}
};JavaScript
/**
* @param {string[]} bank
* @return {number}
*/
var numberOfBeams = function(bank) {
let ans = 0;
let pre = 0;
for (let row of bank) {
let cur = row.split("").filter(x => x === "1").length;
if (cur > 0) {
ans += pre * cur;
pre = cur;
}
}
return ans;
};Go
func numberOfBeams(bank []string) int {
ans, pre := 0, 0
for _, row := range bank {
cur := strings.Count(row, "1")
if cur > 0 {
ans += pre * cur
pre = cur
}
}
return ans
}These code snippets demonstrate the efficient iterative approach to solving the problem, ensuring both accuracy and optimal performance. Remember that the choice of language may slightly affect the exact syntax, but the underlying algorithm remains consistent for all implementations.