- {x}
- Minimum Number of Steps to Make Two Strings Anagram II
- Minimum Time to Complete Trips
- Minimum Time to Finish the Race
- Number of Ways to Build House of Cards
- Most Frequent Number Following Key In an Array
- Sort the Jumbled Numbers
- All Ancestors of a Node in a Directed Acyclic Graph
- Minimum Number of Moves to Make Palindrome
- Cells in a Range on an Excel Sheet
- Append K Integers With Minimal Sum
- Create Binary Tree From Descriptions
- Replace Non-Coprime Numbers in Array
- Number of Single Divisor Triplets
- Finding the Topic of Each Post
- Find All K-Distant Indices in an Array
- Count Artifacts That Can Be Extracted
- Maximize the Topmost Element After K Moves
- Read More...

Cells in a Range on an Excel Sheet
A cell (r, c) of an excel sheet is represented as a string "<col><row>" where:
<col>denotes the column numbercof the cell. It is represented by alphabetical letters.- For example, the
1stcolumn is denoted by'A', the2ndby'B', the3rdby'C', and so on.
- For example, the
<row>is the row numberrof the cell. Therthrow is represented by the integerr.
You are given a string s in the format "<col1><row1>:<col2><row2>", where <col1> represents the column c1, <row1> represents the row r1, <col2> represents the column c2, and <row2> represents the row r2, such that r1 <= r2 and c1 <= c2.
Return the list of cells (x, y) such that r1 <= x <= r2 and c1 <= y <= c2. The cells should be represented as strings in the format mentioned above and be sorted in non-decreasing order first by columns and then by rows.
Example 1:
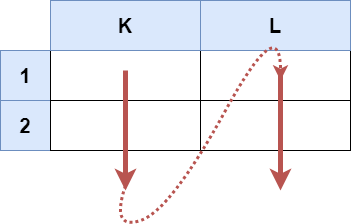
Input: s = "K1:L2" Output: ["K1","K2","L1","L2"] Explanation: The above diagram shows the cells which should be present in the list. The red arrows denote the order in which the cells should be presented.
Example 2:

Input: s = "A1:F1" Output: ["A1","B1","C1","D1","E1","F1"] Explanation: The above diagram shows the cells which should be present in the list. The red arrow denotes the order in which the cells should be presented.
Constraints:
s.length == 5'A' <= s[0] <= s[3] <= 'Z''1' <= s[1] <= s[4] <= '9'sconsists of uppercase English letters, digits and':'.
Solution Explanation:
The problem asks to generate a list of cell names in an Excel sheet given a range specified in the format "col1row1:col2row2". The solution involves iterating through all cells within the specified range and constructing their names.
Approach:
-
Parsing the Input: The input string
sis of the format "col1row1:col2row2". We extractcol1,row1,col2, androw2. Note that column names are represented by characters (A, B, C,...), while row numbers are integers. -
Iterating through the Range: We use nested loops to iterate through all cells within the specified range. The outer loop iterates through columns from
col1tocol2, and the inner loop iterates through rows fromrow1torow2. -
Generating Cell Names: Inside the inner loop, we construct the cell name by concatenating the current column character and the current row number.
-
Storing and Returning: We append each generated cell name to a list. Finally, this list of cell names is returned.
Code Explanation (Python):
class Solution:
def cellsInRange(self, s: str) -> List[str]:
col1, row1, col2, row2 = ord(s[0]), int(s[1]), ord(s[3]), int(s[4]) #Extract col and row values. ord converts char to ASCII value.
result = []
for col in range(col1, col2 + 1):
for row in range(row1, row2 + 1):
result.append(chr(col) + str(row)) # chr converts ASCII value to char.
return resultExplanation of each part:
-
col1, row1, col2, row2 = ord(s[0]), int(s[1]), ord(s[3]), int(s[4]): This line extracts the start and end column and row numbers from the input strings.ord()converts a character to its ASCII integer representation. We use these ASCII values to iterate through the column range. -
result = []: Initializes an empty list to store the generated cell names. -
for col in range(col1, col2 + 1):: The outer loop iterates through columns fromcol1tocol2(inclusive). -
for row in range(row1, row2 + 1):: The inner loop iterates through rows fromrow1torow2(inclusive). -
result.append(chr(col) + str(row)): This line constructs the cell name by converting the ASCII column value back to a character usingchr()and converting the row number to a string usingstr(). The cell name is then appended to theresultlist. -
return result: The function returns the list of generated cell names.
Time and Space Complexity Analysis:
Time Complexity: O(mn), where 'm' is the number of columns in the range (col2 - col1 + 1) and 'n' is the number of rows in the range (row2 - row1 + 1). This is because the nested loops iterate through all cells in the specified range.
Space Complexity: O(mn), as the space used to store the result list is proportional to the number of cells in the range. In the worst case, this could be up to 26*9 = 234 cells for a range like "A1:Z9".
The code in other languages (Java, C++, Go, TypeScript) follows a very similar approach, with only minor syntactic differences. The time and space complexities remain the same.