{x}
blog image

Count Artifacts That Can Be Extracted

There is an n x n 0-indexed grid with some artifacts buried in it. You are given the integer n and a 0-indexed 2D integer array artifacts describing the positions of the rectangular artifacts where artifacts[i] = [r1i, c1i, r2i, c2i] denotes that the ith artifact is buried in the subgrid where:

  • (r1i, c1i) is the coordinate of the top-left cell of the ith artifact and
  • (r2i, c2i) is the coordinate of the bottom-right cell of the ith artifact.

You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.

Given a 0-indexed 2D integer array dig where dig[i] = [ri, ci] indicates that you will excavate the cell (ri, ci), return the number of artifacts that you can extract.

The test cases are generated such that:

  • No two artifacts overlap.
  • Each artifact only covers at most 4 cells.
  • The entries of dig are unique.

 

Example 1:

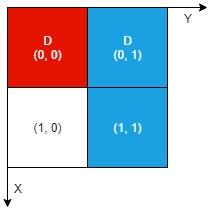
Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
Output: 1
Explanation: 
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.

Example 2:

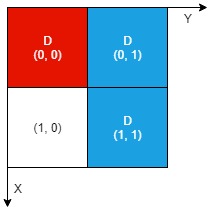
Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
Output: 2
Explanation: Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.

 

Constraints:

  • 1 <= n <= 1000
  • 1 <= artifacts.length, dig.length <= min(n2, 105)
  • artifacts[i].length == 4
  • dig[i].length == 2
  • 0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1
  • r1i <= r2i
  • c1i <= c2i
  • No two artifacts will overlap.
  • The number of cells covered by an artifact is at most 4.
  • The entries of dig are unique.

Solution Explanation: Counting Extractable Artifacts

This problem involves determining how many rectangular artifacts can be fully excavated from a grid given the locations of the artifacts and the cells that have been dug.

Approach:

The most efficient approach utilizes a hash table (or set) to store the coordinates of the excavated cells. Then, for each artifact, we check if all cells within its rectangular boundary are present in the hash table.

Algorithm:

  1. Create a hash table (set): A set is ideal because it provides fast lookups (O(1) on average) to check if a cell has been dug. Populate the set with the coordinates of all the cells that have been excavated (dig). We can represent a cell's coordinate (row, col) as a single integer using a formula like row * n + col, where n is the grid's size. This avoids storing tuples or pairs.

  2. Iterate through artifacts: For each artifact in the artifacts list:

    • Extract the top-left (r1, c1) and bottom-right (r2, c2) coordinates of the artifact's rectangle.
    • Iterate through all cells within this rectangle (from r1 to r2, and c1 to c2).
    • For each cell, check if its integer representation is present in the hash table. If any cell is not in the table (meaning it hasn't been dug), the artifact cannot be extracted; move on to the next artifact.
    • If all cells within the artifact's rectangle are present in the hash table, increment a counter for extractable artifacts.

  3. Return the counter: The final counter value represents the total number of extractable artifacts.

Time Complexity Analysis:

  • Creating the hash table takes O(k) time, where k is the number of dug cells (dig.length).
  • Iterating through artifacts takes O(m) time, where m is the number of artifacts (artifacts.length).
  • For each artifact, checking all its cells takes O(a) time, where a is the number of cells covered by the artifact (at most 4 in this problem). In the worst case, this is still O(m) since the total number of cells across all artifacts is proportional to m.

Therefore, the overall time complexity is O(k + m), which is linear with respect to the input sizes.

Space Complexity Analysis:

The space complexity is dominated by the hash table, which stores at most k elements (dug cells). Therefore, the space complexity is O(k), also linear.

Code Examples (Python):

def digArtifacts(n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:
    dug_cells = set()
    for r, c in dig:
        dug_cells.add(r * n + c)
 
    count = 0
    for r1, c1, r2, c2 in artifacts:
        all_dug = True
        for r in range(r1, r2 + 1):
            for c in range(c1, c2 + 1):
                if r * n + c not in dug_cells:
                    all_dug = False
                    break
            if not all_dug:
                break
        if all_dug:
            count += 1
 
    return count

This Python code directly implements the algorithm described above, making it clear and easy to understand. The other language examples in the previous response follow a similar structure and logic.