{x}
blog image

Where Will the Ball Fall

You have a 2-D grid of size m x n representing a box, and you have n balls. The box is open on the top and bottom sides.

Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.

  • A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as 1.
  • A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as -1.

We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V" shaped pattern between two boards or if a board redirects the ball into either wall of the box.

Return an array answer of size n where answer[i] is the column that the ball falls out of at the bottom after dropping the ball from the ith column at the top, or -1 if the ball gets stuck in the box.

 

Example 1:

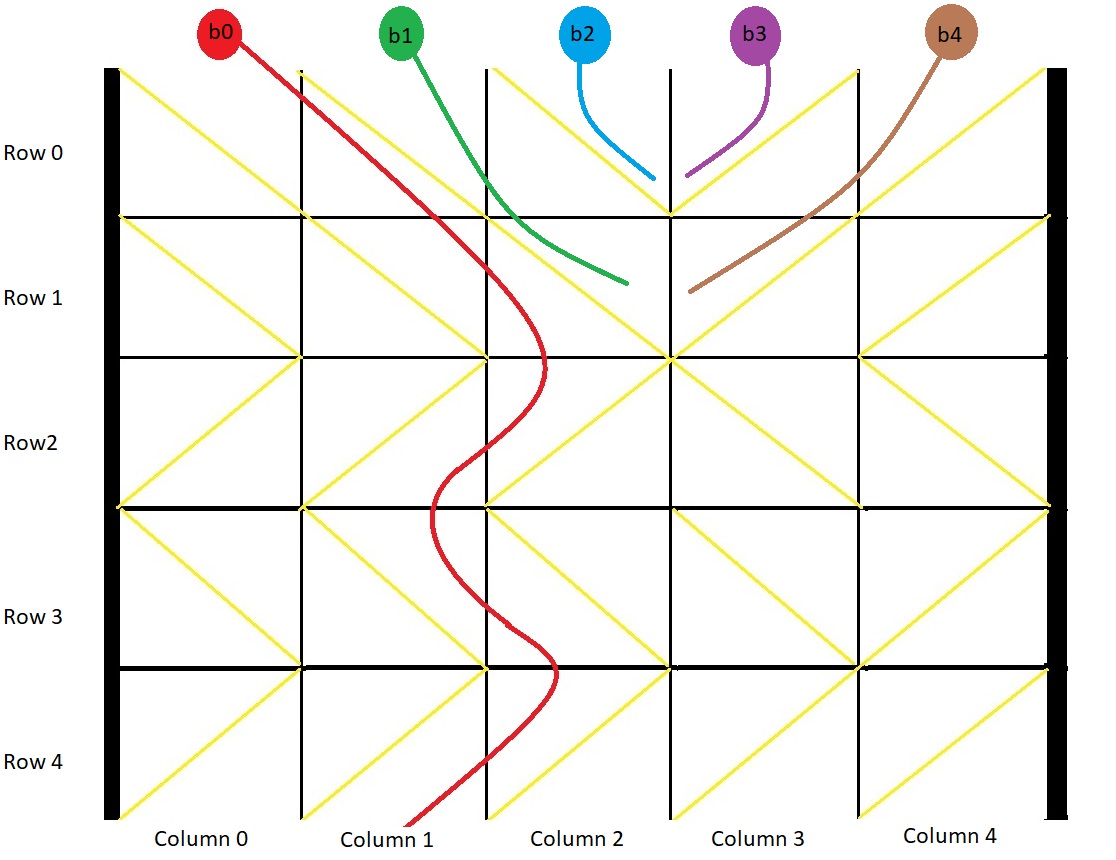
Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
Output: [1,-1,-1,-1,-1]
Explanation: This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.

Example 2:

Input: grid = [[-1]]
Output: [-1]
Explanation: The ball gets stuck against the left wall.

Example 3:

Input: grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
Output: [0,1,2,3,4,-1]

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100
  • grid[i][j] is 1 or -1.

1706. Where Will the Ball Fall

Problem Description

You are given an m x n grid representing a box with balls dropped from the top. Each cell contains a diagonal board that redirects the ball either to the right (1) or to the left (-1). A ball gets stuck if it hits a "V" shaped pattern or a wall. The task is to determine the column each ball falls out of at the bottom, or -1 if it gets stuck.

The most intuitive way to solve this problem is to simulate the ball's movement. We can use Depth-First Search (DFS) to track each ball's path.

For each ball dropped from the top (one ball per column), we recursively trace its movement downwards:

  1. Base Case: If the ball reaches the bottom row (i == m), it falls out at the current column j, so we return j.
  2. Stuck Conditions: The ball gets stuck if:
    • It's in the leftmost column (j == 0) and the board directs it left (grid[i][j] == -1).
    • It's in the rightmost column (j == n - 1) and the board directs it right (grid[i][j] == 1).
    • The board directs it right, but the next cell to the right directs it left (grid[i][j] == 1 && grid[i][j + 1] == -1).
    • The board directs it left, but the next cell to the left directs it right (grid[i][j] == -1 && grid[i][j - 1] == 1). If any of these conditions are true, we return -1.
  3. Recursive Step: Otherwise, the ball moves to the next row based on the board's direction:
    • If grid[i][j] == 1, it moves right (dfs(i + 1, j + 1)).
    • If grid[i][j] == -1, it moves left (dfs(i + 1, j - 1)).

The dfs function recursively simulates the ball's trajectory. The main function iterates through each column, dropping a ball and using dfs to find its final position or determine if it gets stuck.

Time and Space Complexity Analysis

  • Time Complexity: O(m * n), where 'm' is the number of rows and 'n' is the number of columns. In the worst case, each ball might traverse all rows.
  • Space Complexity: O(m) due to the recursive depth of the DFS calls. The recursion depth is at most 'm' (the number of rows).

Code Implementation (Python)

class Solution:
    def findBall(self, grid: List[List[int]]) -> List[int]:
        m, n = len(grid), len(grid[0])
        
        def dfs(i: int, j: int) -> int:
            if i == m:
                return j
            if j == 0 and grid[i][j] == -1:
                return -1
            if j == n - 1 and grid[i][j] == 1:
                return -1
            if grid[i][j] == 1 and grid[i][j + 1] == -1:
                return -1
            if grid[i][j] == -1 and grid[i][j - 1] == 1:
                return -1
            return dfs(i + 1, j + 1) if grid[i][j] == 1 else dfs(i + 1, j - 1)
 
        return [dfs(0, j) for j in range(n)]

The Python code directly implements the DFS approach described above. Other languages (Java, C++, JavaScript, etc.) would have similar implementations, following the same logic. The key is the recursive dfs function that simulates the ball's path and handles the stuck conditions.