{x}
blog image

Walking Robot Simulation II

A width x height grid is on an XY-plane with the bottom-left cell at (0, 0) and the top-right cell at (width - 1, height - 1). The grid is aligned with the four cardinal directions ("North", "East", "South", and "West"). A robot is initially at cell (0, 0) facing direction "East".

The robot can be instructed to move for a specific number of steps. For each step, it does the following.

  1. Attempts to move forward one cell in the direction it is facing.
  2. If the cell the robot is moving to is out of bounds, the robot instead turns 90 degrees counterclockwise and retries the step.

After the robot finishes moving the number of steps required, it stops and awaits the next instruction.

Implement the Robot class:

  • Robot(int width, int height) Initializes the width x height grid with the robot at (0, 0) facing "East".
  • void step(int num) Instructs the robot to move forward num steps.
  • int[] getPos() Returns the current cell the robot is at, as an array of length 2, [x, y].
  • String getDir() Returns the current direction of the robot, "North", "East", "South", or "West".

 

Example 1:

example-1 
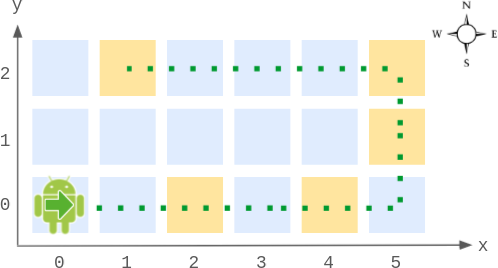
Input
["Robot", "step", "step", "getPos", "getDir", "step", "step", "step", "getPos", "getDir"]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
Output
[null, null, null, [4, 0], "East", null, null, null, [1, 2], "West"]

Explanation
Robot robot = new Robot(6, 3); // Initialize the grid and the robot at (0, 0) facing East.
robot.step(2);  // It moves two steps East to (2, 0), and faces East.
robot.step(2);  // It moves two steps East to (4, 0), and faces East.
robot.getPos(); // return [4, 0]
robot.getDir(); // return "East"
robot.step(2);  // It moves one step East to (5, 0), and faces East.
                // Moving the next step East would be out of bounds, so it turns and faces North.
                // Then, it moves one step North to (5, 1), and faces North.
robot.step(1);  // It moves one step North to (5, 2), and faces North (not West).
robot.step(4);  // Moving the next step North would be out of bounds, so it turns and faces West.
                // Then, it moves four steps West to (1, 2), and faces West.
robot.getPos(); // return [1, 2]
robot.getDir(); // return "West"

 

Constraints:

  • 2 <= width, height <= 100
  • 1 <= num <= 105
  • At most 104 calls in total will be made to step, getPos, and getDir.

Solution Explanation for Walking Robot Simulation II

This problem simulates a robot moving on a grid, with the robot turning counter-clockwise if it hits a boundary. The solution involves careful tracking of the robot's position, direction, and boundary conditions.

Approach

The core idea is to maintain the robot's state: its current x and y coordinates, its current direction, and the grid dimensions. The step function iteratively moves the robot one step at a time, checking for boundary conditions at each step. If the robot attempts to move out of bounds, its direction is updated, and the step is retried.

The directions are represented as integers (0: East, 1: North, 2: West, 3: South), which allows for easy rotation using modulo arithmetic.

Code (Python3)

class Robot:
    def __init__(self, width: int, height: int):
        self.width = width
        self.height = height
        self.x = 0
        self.y = 0
        self.dir = 0  # 0: East, 1: North, 2: West, 3: South
 
    def step(self, num: int) -> None:
        dx = [1, 0, -1, 0]  # Change in x for each direction
        dy = [0, 1, 0, -1]  # Change in y for each direction
 
        for _ in range(num):
            nx = self.x + dx[self.dir]
            ny = self.y + dy[self.dir]
 
            if 0 <= nx < self.width and 0 <= ny < self.height:
                self.x = nx
                self.y = ny
            else:
                self.dir = (self.dir + 1) % 4  # Turn counter-clockwise
 
    def getPos(self) -> List[int]:
        return [self.x, self.y]
 
    def getDir(self) -> str:
        directions = ["East", "North", "West", "South"]
        return directions[self.dir]

Code (Java)

class Robot {
    private int width;
    private int height;
    private int x;
    private int y;
    private int dir; // 0: East, 1: North, 2: West, 3: South
 
    public Robot(int width, int height) {
        this.width = width;
        this.height = height;
        this.x = 0;
        this.y = 0;
        this.dir = 0;
    }
 
    public void step(int num) {
        int[] dx = {1, 0, -1, 0}; // Change in x for each direction
        int[] dy = {0, 1, 0, -1}; // Change in y for each direction
 
        for (int i = 0; i < num; i++) {
            int nx = x + dx[dir];
            int ny = y + dy[dir];
 
            if (nx >= 0 && nx < width && ny >= 0 && ny < height) {
                x = nx;
                y = ny;
            } else {
                dir = (dir + 1) % 4; // Turn counter-clockwise
            }
        }
    }
 
    public int[] getPos() {
        return new int[]{x, y};
    }
 
    public String getDir() {
        String[] directions = {"East", "North", "West", "South"};
        return directions[dir];
    }
}

Code (C++)

class Robot {
public:
    int width;
    int height;
    int x;
    int y;
    int dir; // 0: East, 1: North, 2: West, 3: South
 
    Robot(int width, int height) {
        this->width = width;
        this->height = height;
        this->x = 0;
        this->y = 0;
        this->dir = 0;
    }
 
    void step(int num) {
        int dx[] = {1, 0, -1, 0}; // Change in x for each direction
        int dy[] = {0, 1, 0, -1}; // Change in y for each direction
 
        for (int i = 0; i < num; i++) {
            int nx = x + dx[dir];
            int ny = y + dy[dir];
 
            if (nx >= 0 && nx < width && ny >= 0 && ny < height) {
                x = nx;
                y = ny;
            } else {
                dir = (dir + 1) % 4; // Turn counter-clockwise
            }
        }
    }
 
    vector<int> getPos() {
        return {x, y};
    }
 
    string getDir() {
        string directions[] = {"East", "North", "West", "South"};
        return directions[dir];
    }
};

Code (Go)

type Robot struct {
	width, height, x, y, dir int // dir: 0-East, 1-North, 2-West, 3-South
}
 
func Constructor(width, height int) Robot {
	return Robot{width, height, 0, 0, 0}
}
 
func (r *Robot) Step(num int) {
	dx := []int{1, 0, -1, 0}
	dy := []int{0, 1, 0, -1}
	for i := 0; i < num; i++ {
		nx, ny := r.x+dx[r.dir], r.y+dy[r.dir]
		if nx >= 0 && nx < r.width && ny >= 0 && ny < r.height {
			r.x, r.y = nx, ny
		} else {
			r.dir = (r.dir + 1) % 4
		}
	}
}
 
func (r *Robot) GetPos() []int {
	return []int{r.x, r.y}
}
 
func (r *Robot) GetDir() string {
	dirs := []string{"East", "North", "West", "South"}
	return dirs[r.dir]
}

Time and Space Complexity

  • Time Complexity: The step function has a time complexity of O(num), where num is the number of steps. The getPos and getDir functions are O(1).
  • Space Complexity: The space complexity is O(1) as it uses a constant amount of extra space to store the robot's state. The space used by the Robot object itself is also constant.

The overall solution is efficient and effectively handles the robot's movement and boundary conditions.