{x}
blog image

Decode the Slanted Ciphertext

A string originalText is encoded using a slanted transposition cipher to a string encodedText with the help of a matrix having a fixed number of rows rows.

originalText is placed first in a top-left to bottom-right manner.

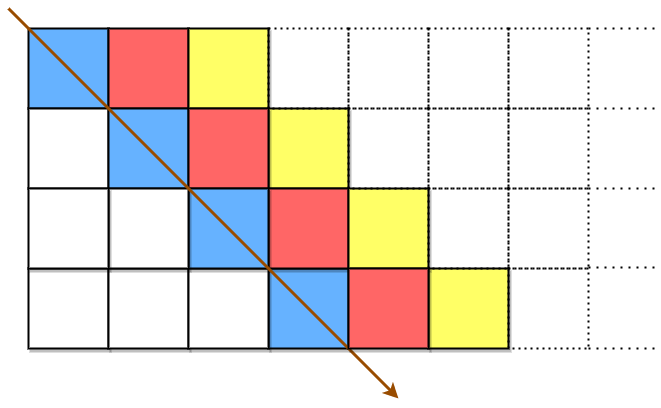
The blue cells are filled first, followed by the red cells, then the yellow cells, and so on, until we reach the end of originalText. The arrow indicates the order in which the cells are filled. All empty cells are filled with ' '. The number of columns is chosen such that the rightmost column will not be empty after filling in originalText.

encodedText is then formed by appending all characters of the matrix in a row-wise fashion.

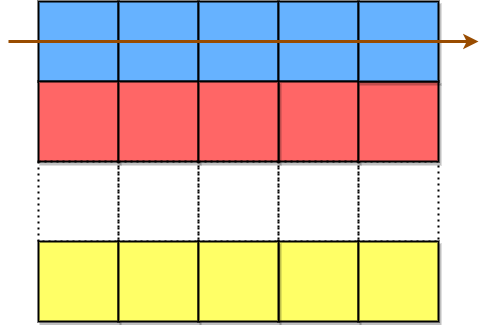
The characters in the blue cells are appended first to encodedText, then the red cells, and so on, and finally the yellow cells. The arrow indicates the order in which the cells are accessed.

For example, if originalText = "cipher" and rows = 3, then we encode it in the following manner:

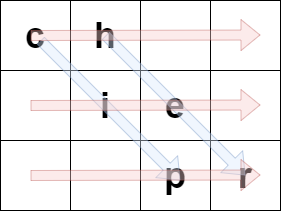
The blue arrows depict how originalText is placed in the matrix, and the red arrows denote the order in which encodedText is formed. In the above example, encodedText = "ch ie pr".

Given the encoded string encodedText and number of rows rows, return the original string originalText.

Note: originalText does not have any trailing spaces ' '. The test cases are generated such that there is only one possible originalText.

 

Example 1:

Input: encodedText = "ch   ie   pr", rows = 3
Output: "cipher"
Explanation: This is the same example described in the problem description.

Example 2:

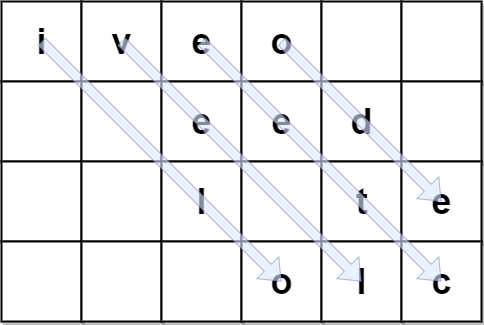
Input: encodedText = "iveo    eed   l te   olc", rows = 4
Output: "i love leetcode"
Explanation: The figure above denotes the matrix that was used to encode originalText. 
The blue arrows show how we can find originalText from encodedText.

Example 3:

Input: encodedText = "coding", rows = 1
Output: "coding"
Explanation: Since there is only 1 row, both originalText and encodedText are the same.

 

Constraints:

  • 0 <= encodedText.length <= 106
  • encodedText consists of lowercase English letters and ' ' only.
  • encodedText is a valid encoding of some originalText that does not have trailing spaces.
  • 1 <= rows <= 1000
  • The testcases are generated such that there is only one possible originalText.

Solution Explanation: Decode the Slanted Ciphertext

This problem involves decoding a slanted transposition cipher. The encoded text (encodedText) was created by writing the original text (originalText) diagonally into a matrix with a given number of rows (rows), then reading the matrix row by row to produce the encoded text. Our task is to reverse this process.

Approach

The core idea is to reconstruct the original text by traversing the matrix diagonally in the reverse order of how it was encoded.

  1. Calculate Columns: First, we determine the number of columns (cols) in the matrix. Since the last column is not empty, we can calculate it as cols = len(encodedText) / rows.

  2. Diagonal Traversal: We iterate through the columns. For each column j, we start at the top-leftmost cell (0, j) and move diagonally down and to the right (x+1, y+1) until we reach the bottom of the matrix or the right edge. As we move, we append the character at each cell to our result.

  3. Remove Trailing Spaces: Finally, we remove any trailing spaces from the resulting string because the problem statement guarantees that originalText does not contain trailing spaces.

Time and Space Complexity

  • Time Complexity: O(n), where n is the length of encodedText. This is because we iterate through the encoded text once to reconstruct the original text.

  • Space Complexity: O(n) in the worst case, as we store the reconstructed string in a StringBuilder or similar data structure. In some implementations, less space might be used if the original string is modified directly.

Code Implementation (Python)

class Solution:
    def decodeCiphertext(self, encodedText: str, rows: int) -> str:
        ans = []
        cols = len(encodedText) // rows  # Integer division to get the number of cols
        for j in range(cols): # Iterate through columns
            x, y = 0, j #Start at the top of each column
            while x < rows and y < cols: #Move diagonally down and right until the end of matrix or column
                ans.append(encodedText[x * cols + y]) #Add character to the result
                x += 1
                y += 1
        return "".join(ans).rstrip() #Join the characters and remove trailing spaces

The other languages (Java, C++, Go, TypeScript) follow a very similar structure. They all perform the diagonal traversal and handle trailing spaces similarly. The core logic remains consistent across languages; only the syntax changes.

Example Walkthrough (Python)

Let's trace the Python code with encodedText = "ch ie pr" and rows = 3.

  1. cols becomes len("ch ie pr") // 3 = 6 // 3 = 2.

  2. The outer loop iterates through columns (j = 0, 1).

  3. j = 0: The inner loop starts at (0, 0). It adds 'c', then moves to (1, 1) adding 'i', then (2, 2) adding 'p'.

  4. j = 1: The inner loop starts at (0, 1). It adds 'h', then moves to (1, 2) adding 'e', then (2, 3) adding 'r'.

  5. "".join(ans) gives "cipher", and .rstrip() removes no trailing spaces in this case. The function returns "cipher".

This approach efficiently reconstructs the original text from the slanted cipher, demonstrating a clear understanding of the encoding process and its reversal.