{x}
blog image

Trapping Rain Water II

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

 

Example 1:

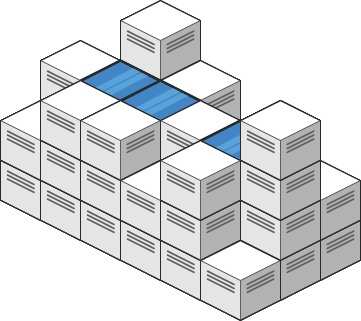
Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

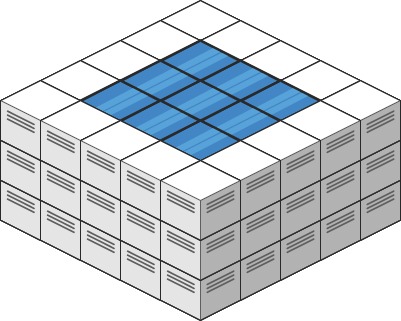
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

 

Constraints:

  • m == heightMap.length
  • n == heightMap[i].length
  • 1 <= m, n <= 200
  • 0 <= heightMap[i][j] <= 2 * 104

Solution Explanation: Trapping Rain Water II

This problem asks to find the volume of rainwater trapped in a 2D elevation map. The key idea is to use a priority queue (min-heap) to process cells in increasing order of height, ensuring that we always consider cells with lower heights first, mimicking the water filling process.

Algorithm:

  1. Initialization:

    • Create a boolean matrix vis to track visited cells (initially all false).
    • Create a min-heap pq to store cells. Initially, add all boundary cells to pq with their heights as priorities. Mark these boundary cells as visited in vis.

  2. Iteration:

    • While the priority queue is not empty:
      • Pop the cell with the minimum height from pq (let's call it (i, j) with height h).
      • For each unvisited neighbor (x, y) of (i, j):
        • Calculate the water trapped at (x, y): max(0, h - heightMap[x][y]). Add this to the total trapped water ans.
        • Mark (x, y) as visited (vis[x][y] = True).
        • Push (x, y) into pq with a priority of max(h, heightMap[x][y]). This ensures that the next time we process a neighbor, its height (or the height of its higher neighbor) is used for determining the trapped water.

  3. Return: Return the total trapped water ans.

Time Complexity Analysis:

  • Each cell is added to and removed from the priority queue at most once.
  • The priority queue operations (insertion and deletion) take O(log(M*N)) time, where M and N are the dimensions of the matrix.
  • The total number of cells is M*N.
  • Therefore, the overall time complexity is O(MN log(MN)).

Space Complexity Analysis:

  • We use a boolean matrix vis of size MN to keep track of visited cells, O(MN).
  • The priority queue can, in the worst case, contain all cells (MN), so its space complexity is O(MN).
  • Therefore, the overall space complexity is O(M*N).

Code in Different Languages:

The provided code snippets (Python, Java, C++, Go) follow the algorithm described above. They use a min-heap (priority queue) data structure to efficiently process cells in ascending order of height. The dirs array helps to efficiently iterate over the four neighboring cells of a given cell. The use of vis ensures we don't process the same cell multiple times, preventing infinite loops. The Go code also demonstrates the implementation of a min-heap using a custom type and the heap package. The choice of language impacts the syntax but the core algorithm remains the same.