- {x}
- Rotate Function
- Integer Replacement
- Random Pick Index
- Evaluate Division
- Nth Digit
- Binary Watch
- Remove K Digits
- Frog Jump
- Sum of Left Leaves
- Convert a Number to Hexadecimal
- Queue Reconstruction by Height
- Trapping Rain Water II
- Valid Word Abbreviation
- Longest Palindrome
- Split Array Largest Sum
- Minimum Unique Word Abbreviation
- Fizz Buzz
- Read More...

Sum of Left Leaves
Given the root of a binary tree, return the sum of all left leaves.
A leaf is a node with no children. A left leaf is a leaf that is the left child of another node.
Example 1:
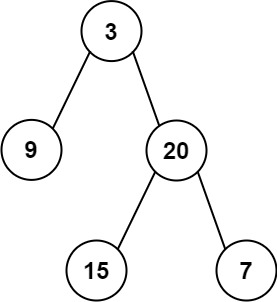
Input: root = [3,9,20,null,null,15,7] Output: 24 Explanation: There are two left leaves in the binary tree, with values 9 and 15 respectively.
Example 2:
Input: root = [1] Output: 0
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. -1000 <= Node.val <= 1000
Solution Explanation: Sum of Left Leaves
The problem asks to find the sum of values of all left leaves in a given binary tree. A left leaf is a node that is a leaf (has no children) and is the left child of its parent.
Two approaches are presented: recursion and iteration using a stack. Both have the same time and space complexity.
Approach 1: Recursion
This approach uses a recursive function to traverse the tree. The core logic is:
-
Base Case: If the current node (
root) isnull, the sum is 0. -
Recursive Step:
- Recursively calculate the sum of left leaves in the right subtree.
- Check if the current node has a left child.
- If it has a left child, check if that left child is a leaf node (both
left.leftandleft.rightarenull). - If it's a leaf, add its value to the sum.
- If it's not a leaf, recursively calculate the sum of left leaves in the left subtree and add it to the total.
-
Return the Sum: The function returns the accumulated sum.
Time Complexity: O(N), where N is the number of nodes in the tree. Each node is visited once.
Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be equal to N.
Approach 2: Iteration using Stack
This approach achieves the same result iteratively using a stack. The steps are:
-
Initialization: Initialize the sum (
ans) to 0 and create a stack containing the root node. -
Iteration: While the stack is not empty:
- Pop a node from the stack.
- Check if it has a left child. If it does:
- If the left child is a leaf, add its value to
ans. - Otherwise, push the left child onto the stack.
- If the left child is a leaf, add its value to
- If the node has a right child, push it onto the stack.
-
Return the Sum: Return the final sum.
Time Complexity: O(N). Each node is visited once.
Space Complexity: O(W), where W is the maximum width of the tree. This is the space used by the stack. In the worst case (a full binary tree), W can be proportional to N. In a skewed tree, W is at most the height of the tree.
Code Examples (Python)
Approach 1 (Recursive):
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def sumOfLeftLeaves(self, root: TreeNode) -> int:
if not root:
return 0
ans = self.sumOfLeftLeaves(root.right)
if root.left:
if not root.left.left and not root.left.right:
ans += root.left.val
else:
ans += self.sumOfLeftLeaves(root.left)
return ans
Approach 2 (Iterative with Stack):
class Solution:
def sumOfLeftLeaves(self, root: TreeNode) -> int:
if not root:
return 0
ans = 0
stack = [root]
while stack:
node = stack.pop()
if node.left:
if not node.left.left and not node.left.right:
ans += node.left.val
else:
stack.append(node.left)
if node.right:
stack.append(node.right)
return ansThe code in other languages (Java, C++, Go, TypeScript, Rust, C) follows similar logic to these Python examples, adapting syntax and data structures as needed for each language. The core algorithmic approach remains consistent.