- {x}
- Most Profit Assigning Work
- Making A Large Island
- Count Unique Characters of All Substrings of a Given String
- Consecutive Numbers Sum
- Positions of Large Groups
- Masking Personal Information
- Flipping an Image
- Find And Replace in String
- Sum of Distances in Tree
- Image Overlap
- Rectangle Overlap
- New 21 Game
- Push Dominoes
- Similar String Groups
- Magic Squares In Grid
- Keys and Rooms
- Split Array into Fibonacci Sequence
- Read More...

Sum of Distances in Tree
There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.
You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.
Example 1:
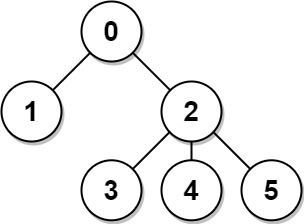
Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]] Output: [8,12,6,10,10,10] Explanation: The tree is shown above. We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) equals 1 + 1 + 2 + 2 + 2 = 8. Hence, answer[0] = 8, and so on.
Example 2:

Input: n = 1, edges = [] Output: [0]
Example 3:
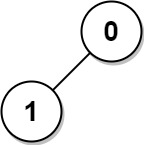
Input: n = 2, edges = [[1,0]] Output: [1,1]
Constraints:
1 <= n <= 3 * 104edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != bi- The given input represents a valid tree.
Solution Explanation: Sum of Distances in Tree
This problem asks to calculate the sum of distances from each node to all other nodes in a tree. A straightforward approach of calculating distances for each node individually would result in O(n^2) time complexity. However, a more efficient solution utilizes a clever tree DP (Dynamic Programming) technique with re-rooting.
Algorithm:
The algorithm consists of two main Depth-First Search (DFS) traversals:
DFS1 (Preprocessing):
-
Initialization: We start from an arbitrary root node (usually node 0). We maintain
ans[0], which initially stores the total distance from the root to all other nodes, andsize[i], an array storing the size of the subtree rooted at nodei(includingiitself). -
Recursive Traversal: The DFS explores the tree recursively. For each node
iand its parentfa:- It adds the current distance
dfrom the root toans[0]. - It initializes
size[i]to 1 (representing the node itself). - It recursively calls
dfs1for each child nodej(not equal to the parentfa), updatingdfor each child and accumulating the subtree sizes.
- It adds the current distance
DFS2 (Re-rooting):
-
Initialization:
ans[i]will store the final answer (sum of distances from nodeito all others).dfs2is called initially with node 0 and its previously calculated total distanceans[0]. -
Recursive Traversal: The DFS recursively traverses the tree, changing the root from one node to another. For each node
iand its child nodej:- It updates
ans[i]to be the current total distancet. - It recursively calls
dfs2for childj. When moving the root fromitoj, the change in total distances is calculated as:t - size[j] + (n - size[j]). This is because:- The distances to nodes in
j's subtree decrease bysize[j]. - The distances to nodes outside
j's subtree increase bysize[j](because they are now one step farther from the new root).
- The distances to nodes in
- It updates
Time Complexity Analysis:
dfs1anddfs2each traverse the tree once. Therefore, the overall time complexity is O(n), where n is the number of nodes.
Space Complexity Analysis:
- We use arrays
ansandsizeof size n, and the recursive call stack can go as deep as n in the worst case (a skewed tree). Hence, the space complexity is O(n).
Code Examples:
The code examples in Python3, Java, C++, Go, and TypeScript provided earlier all follow this algorithm. They are well-commented and easy to understand. The key lies in the understanding of the re-rooting step in dfs2 and the formula t - size[j] + n - size[j] which efficiently updates the total distances when the root changes.