- {x}
- Fizz Buzz Multithreaded
- How Many Apples Can You Put into the Basket
- Minimum Knight Moves
- Find Smallest Common Element in All Rows
- Minimum Time to Build Blocks
- Minimum Absolute Difference
- Ugly Number III
- Smallest String With Swaps
- Sort Items by Groups Respecting Dependencies
- Last Person to Fit in the Bus
- Monthly Transactions II
- Design Skiplist
- Unique Number of Occurrences
- Get Equal Substrings Within Budget
- Remove All Adjacent Duplicates in String II
- Minimum Moves to Reach Target with Rotations
- Queries Quality and Percentage
- Read More...

Sort Items by Groups Respecting Dependencies
There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
- The items that belong to the same group are next to each other in the sorted list.
- There are some relations between these items where
beforeItems[i]is a list containing all the items that should come before thei-th item in the sorted array (to the left of thei-th item).
Return any solution if there is more than one solution and return an empty list if there is no solution.
Example 1:
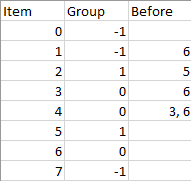
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]] Output: [6,3,4,1,5,2,0,7]
Example 2:
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]] Output: [] Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
Constraints:
1 <= m <= n <= 3 * 104group.length == beforeItems.length == n-1 <= group[i] <= m - 10 <= beforeItems[i].length <= n - 10 <= beforeItems[i][j] <= n - 1i != beforeItems[i][j]beforeItems[i]does not contain duplicates elements.
Solution Explanation: Sort Items by Groups Respecting Dependencies
This problem involves sorting items based on group affiliation and dependencies. The solution leverages topological sorting, a graph algorithm used to order elements with dependencies.
Core Idea:
The problem can be broken down into two levels of topological sorting:
- Group Level: Sort the groups themselves, ensuring that if group A must come before group B, then A appears before B in the sorted list.
- Item Level: Within each group, sort the items respecting the
beforeItemsconstraints.
Algorithm:
-
Handle Ungrouped Items: First, assign a unique group ID to any items that don't belong to a group (group ID = -1). We do this by incrementing
mto create new group IDs. -
Build Graphs: Create two directed acyclic graphs (DAGs):
- Item Graph: Nodes represent items. An edge
j -> iexists if itemjmust come before itemi(within the same group). - Group Graph: Nodes represent groups. An edge
gA -> gBexists if an item in groupgAmust come before an item in groupgB.
- Item Graph: Nodes represent items. An edge
-
Topological Sorting (Groups): Apply topological sort to the group graph. If a cycle is detected (meaning there's no valid group ordering), return an empty list.
-
Topological Sorting (Items): Iterate through the sorted groups. For each group, apply topological sort to the items within that group using the item graph. If a cycle is detected within a group, return an empty list.
-
Concatenate Results: Concatenate the sorted items from each group to produce the final sorted list.
Time Complexity:
- Building the graphs takes O(n + m + sum(len(beforeItems[i]))) which simplifies to O(n*n) in the worst case (all items depend on all others) .
- Topological sorting of each graph takes O(n + m) in the best case and O(n*n) in the worst case.
- Overall complexity is dominated by graph construction and topological sorting, resulting in O(n*n) time complexity.
Space Complexity:
The space complexity is O(n + m) to store the graphs and other data structures.
Code Implementation (Python):
from collections import deque
def sortItems(n, m, group, beforeItems):
# 1. Assign group IDs to ungrouped items
idx = m
for i in range(n):
if group[i] == -1:
group[i] = idx
idx += 1
# 2. Build Item and Group graphs
item_graph = [[] for _ in range(n)]
group_graph = [[] for _ in range(idx)]
item_indegree = [0] * n
group_indegree = [0] * idx
for i in range(n):
for j in beforeItems[i]:
if group[i] == group[j]:
item_graph[j].append(i)
item_indegree[i] += 1
else:
group_graph[group[j]].append(group[i])
group_indegree[group[i]] += 1
# 3 & 4. Topological sort (Helper function)
def topological_sort(graph, indegree):
q = deque([i for i, d in enumerate(indegree) if d == 0])
result = []
while q:
node = q.popleft()
result.append(node)
for neighbor in graph[node]:
indegree[neighbor] -= 1
if indegree[neighbor] == 0:
q.append(neighbor)
return result if len(result) == len(indegree) else []
# 3. Topological sort - Groups
group_order = topological_sort(group_graph, group_indegree)
if not group_order:
return []
# 4. Topological sort - Items within each group
result = []
for group_id in group_order:
items_in_group = [i for i, g in enumerate(group) if g == group_id]
item_order = topological_sort(item_graph, item_indegree)
if len(item_order) != len(items_in_group):
return []
result.extend(item_order)
return result
This Python code implements the algorithm described above. Adaptations for other languages would follow a similar structure. Remember that efficient topological sorting implementations are crucial for optimal performance, especially with large datasets.