{x}
blog image

Smallest Subtree with all the Deepest Nodes

Given the root of a binary tree, the depth of each node is the shortest distance to the root.

Return the smallest subtree such that it contains all the deepest nodes in the original tree.

A node is called the deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.

 

Example 1:

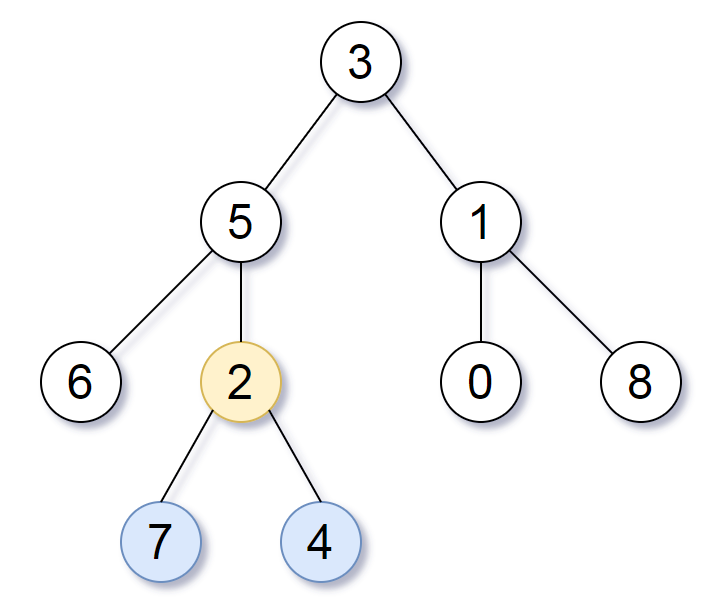
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

 

Constraints:

  • The number of nodes in the tree will be in the range [1, 500].
  • 0 <= Node.val <= 500
  • The values of the nodes in the tree are unique.

 

Note: This question is the same as 1123: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/

Solution Explanation: Smallest Subtree with all Deepest Nodes

This problem asks to find the smallest subtree containing all the deepest nodes in a given binary tree. The solution uses a depth-first search (DFS) approach to efficiently find this subtree.

Approach:

The core idea is to perform a post-order traversal of the tree. For each node, we need to know:

  1. The depth of the subtree rooted at that node: This is calculated recursively by adding 1 to the maximum depth of its left and right subtrees.

  2. The smallest subtree containing all deepest nodes of its subtree: This is the crucial part.

    • If the left subtree is deeper than the right subtree, the smallest subtree is the result from the left subtree.
    • If the right subtree is deeper, the smallest subtree is the result from the right subtree.
    • If both subtrees have the same depth, the current node itself is the smallest subtree because it's the lowest common ancestor of all deepest nodes in its subtree.

Algorithm:

The dfs function recursively processes each node:

  1. Base Case: If the node is null, return null (no subtree) and depth 0.

  2. Recursive Step:

    • Recursively call dfs on the left and right children to get their smallest subtrees (leftSubtree, rightSubtree) and their depths (leftDepth, rightDepth).
    • Compare leftDepth and rightDepth:
      • If leftDepth > rightDepth, the smallest subtree is leftSubtree, and the depth is leftDepth + 1.
      • If leftDepth < rightDepth, the smallest subtree is rightSubtree, and the depth is rightDepth + 1.
      • If leftDepth == rightDepth, the current node is the smallest subtree, and the depth is leftDepth + 1.

  3. Return Value: The function returns a pair: (smallestSubtree, depth).

The main function simply calls dfs(root) and returns the first element of the resulting pair, which is the smallestSubtree.

Time and Space Complexity:

  • Time Complexity: O(N), where N is the number of nodes in the tree. We visit each node exactly once during the DFS traversal.
  • Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be N, resulting in O(N) space complexity. However, for balanced trees, H is log(N), leading to O(log N) space complexity.

Code (Python):

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
 
def subtreeWithAllDeepest(root: TreeNode) -> TreeNode:
    def dfs(node: TreeNode):
        if not node:
            return None, 0  # Return None subtree and depth 0 for empty subtree
        
        left_subtree, left_depth = dfs(node.left)
        right_subtree, right_depth = dfs(node.right)
 
        if left_depth > right_depth:
            return left_subtree, left_depth + 1
        elif right_depth > left_depth:
            return right_subtree, right_depth + 1
        else:
            return node, left_depth + 1
 
    return dfs(root)[0]

The code in other languages (Java, C++, Go, TypeScript) follows the same logic, differing only in syntax. The key is the recursive dfs function and the handling of the different depth cases.