{x}
blog image

Shortest Path to Get All Keys

You are given an m x n grid grid where:

  • '.' is an empty cell.
  • '#' is a wall.
  • '@' is the starting point.
  • Lowercase letters represent keys.
  • Uppercase letters represent locks.

You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.

If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.

For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it is impossible, return -1.

 

Example 1:

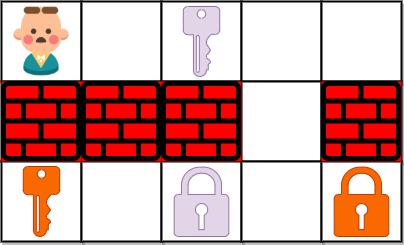
Input: grid = ["@.a..","###.#","b.A.B"]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.

Example 2:

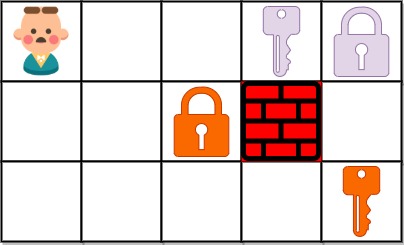
Input: grid = ["@..aA","..B#.","....b"]
Output: 6

Example 3:

Input: grid = ["@Aa"]
Output: -1

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 30
  • grid[i][j] is either an English letter, '.', '#', or '@'. 
  • There is exactly one '@' in the grid.
  • The number of keys in the grid is in the range [1, 6].
  • Each key in the grid is unique.
  • Each key in the grid has a matching lock.

Solution Explanation: Shortest Path to Get All Keys

This problem requires finding the minimum number of moves to collect all keys in a grid, navigating around walls and locks. The solution utilizes a combination of Breadth-First Search (BFS) and bit manipulation for efficient state tracking.

Core Idea:

The key insight is representing the collected keys using a bitmask. Each bit in the bitmask corresponds to a key; a set bit indicates the key is collected, and an unset bit means it's not. This allows us to efficiently track the state of key collection during the search.

Algorithm:

  1. Initialization:

    • Find the starting position ('@') and the total number of keys (k).
    • Create a queue (q) to store search states. Each state is a tuple: (row, col, bitmask).
    • Create a visited set (vis) to avoid revisiting states.

  2. BFS:

    • Enqueue the starting position with an initial bitmask of 0 (no keys collected).
    • While the queue is not empty:
      • Dequeue a state.
      • If the bitmask has all bits set (all keys collected), return the current distance (number of moves).
      • Explore adjacent cells:
        • Check for bounds, walls ('#'), and locks. If a lock is encountered, check if the corresponding key is in the bitmask.
        • If the cell is accessible:
          • Update the bitmask if a key is found.
          • If the new state is not visited:
            • Mark it as visited.
            • Enqueue it.
    • If the loop completes without finding all keys, return -1 (impossible).

Time and Space Complexity:

  • Time Complexity: O(M * N * 2k), where M and N are the grid dimensions, and k is the number of keys. The 2k factor comes from the possible bitmask states. BFS explores all reachable states.

  • Space Complexity: O(M * N * 2k) to store the visited set. The queue size can also reach this order in the worst case.

Code Examples (Python, Java, C++, Go):

The code examples provided earlier effectively implement this algorithm. The core logic remains consistent across languages: BFS with bitmask state representation. The differences primarily lie in syntax and data structure implementations (e.g., deque in Python vs. ArrayDeque in Java). The use of helper functions (pairwise in Python) and efficient data structures are optimizations to improve readability and performance. The comments within the code thoroughly explain each step.