{x}
blog image

Pyramid Transition Matrix

You are stacking blocks to form a pyramid. Each block has a color, which is represented by a single letter. Each row of blocks contains one less block than the row beneath it and is centered on top.

To make the pyramid aesthetically pleasing, there are only specific triangular patterns that are allowed. A triangular pattern consists of a single block stacked on top of two blocks. The patterns are given as a list of three-letter strings allowed, where the first two characters of a pattern represent the left and right bottom blocks respectively, and the third character is the top block.

  • For example, "ABC" represents a triangular pattern with a 'C' block stacked on top of an 'A' (left) and 'B' (right) block. Note that this is different from "BAC" where 'B' is on the left bottom and 'A' is on the right bottom.

You start with a bottom row of blocks bottom, given as a single string, that you must use as the base of the pyramid.

Given bottom and allowed, return true if you can build the pyramid all the way to the top such that every triangular pattern in the pyramid is in allowed, or false otherwise.

 

Example 1:

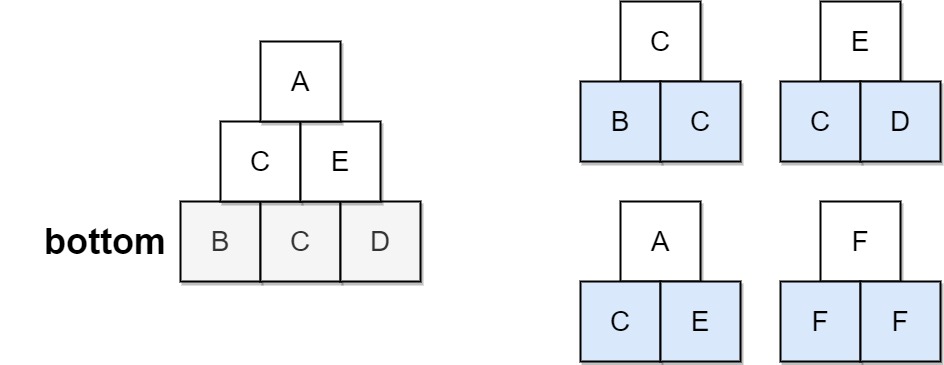
Input: bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"]
Output: true
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 3), we can build "CE" on level 2 and then build "A" on level 1.
There are three triangular patterns in the pyramid, which are "BCC", "CDE", and "CEA". All are allowed.

Example 2:

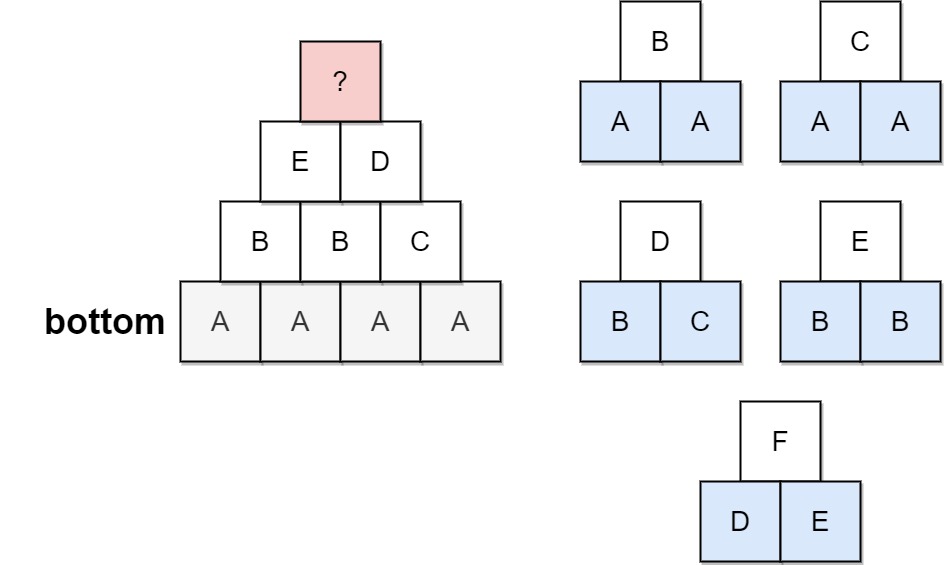
Input: bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"]
Output: false
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 4), there are multiple ways to build level 3, but trying all the possibilites, you will get always stuck before building level 1.

 

Constraints:

  • 2 <= bottom.length <= 6
  • 0 <= allowed.length <= 216
  • allowed[i].length == 3
  • The letters in all input strings are from the set {'A', 'B', 'C', 'D', 'E', 'F'}.
  • All the values of allowed are unique.

Solution Explanation:

This problem asks whether it's possible to build a pyramid using given blocks and allowed triangular patterns. The solution uses Depth-First Search (DFS) with memoization to efficiently explore the possible pyramid constructions.

Approach:

The core idea is to recursively build the pyramid layer by layer, starting from the bottom. At each level, we consider all possible combinations of blocks that can form valid triangular patterns based on the allowed rules. We use DFS to explore all possible combinations and check if it's possible to reach a single block at the top.

Memoization (using @cache in Python or dp in other languages) is crucial for optimization. It stores the results of subproblems (pyramid constructions from intermediate levels) to avoid redundant computations. This significantly improves the efficiency, especially for larger inputs.

Algorithm:

  1. Preprocessing: Create a data structure (dictionary d in Python, array f in Java/C++/Go) to efficiently look up allowed patterns. This avoids repeatedly searching through the allowed list. The key is a pair of bottom blocks, and the value is a set of possible top blocks.

  2. Recursive DFS (dfs function):

    • Base Case: If the current level has only one block, it's a valid pyramid, so return true.
    • Recursive Step: Iterate through the pairs of adjacent blocks in the current level. For each pair, find the possible top blocks from the preprocessed data structure. Generate all possible next-level strings using itertools.product (Python) or explicit loops (other languages). Recursively call dfs for each next-level string. If any recursive call returns true, return true (a valid pyramid is found). Otherwise, return false (no valid pyramid can be built from this level).

  3. Initial Call: Start the DFS with the given bottom string.

Time Complexity Analysis:

  • Preprocessing: O(A), where A is the length of the allowed list. This step builds the lookup table.

  • DFS: The worst-case time complexity depends on the size of the search space. In the worst scenario, the number of possible pyramids can grow exponentially with the length of the bottom string. Let's say the maximum number of possible top blocks for any pair of bottom blocks is k. Then in the worst case, the time complexity could be O(kn), where n is the length of the bottom string. However, the memoization significantly reduces the actual runtime by caching results of subproblems. Without memoization, it would be truly exponential.

Space Complexity Analysis:

The space complexity is dominated by:

  • Memoization table: O(L * kn), where L is the maximum length of a string during DFS, and other parameters are as defined above. However, the actual space used is often much less due to many branches of the search space being pruned.

  • Preprocessing data structure: O(B^2 * k), where B is the number of different blocks (at most 6 in this problem). This represents the space used to store allowed transitions.

In summary, the algorithm's effectiveness relies on the memoization technique to mitigate the exponential worst-case time complexity. The space complexity is also affected by the memoization table but is often significantly smaller than the theoretical worst case due to pruning.