{x}
blog image

Largest Plus Sign

You are given an integer n. You have an n x n binary grid grid with all values initially 1's except for some indices given in the array mines. The ith element of the array mines is defined as mines[i] = [xi, yi] where grid[xi][yi] == 0.

Return the order of the largest axis-aligned plus sign of 1's contained in grid. If there is none, return 0.

An axis-aligned plus sign of 1's of order k has some center grid[r][c] == 1 along with four arms of length k - 1 going up, down, left, and right, and made of 1's. Note that there could be 0's or 1's beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1's.

 

Example 1:

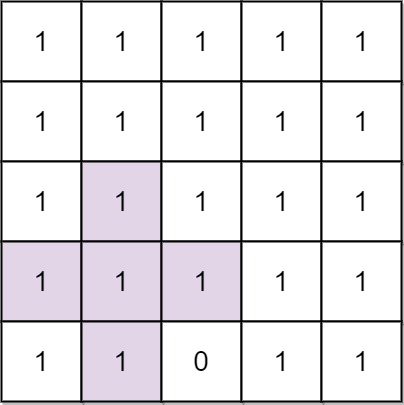
Input: n = 5, mines = [[4,2]]
Output: 2
Explanation: In the above grid, the largest plus sign can only be of order 2. One of them is shown.

Example 2:

Input: n = 1, mines = [[0,0]]
Output: 0
Explanation: There is no plus sign, so return 0.

 

Constraints:

  • 1 <= n <= 500
  • 1 <= mines.length <= 5000
  • 0 <= xi, yi < n
  • All the pairs (xi, yi) are unique.

Solution Explanation for Largest Plus Sign

This problem asks to find the order of the largest plus sign of 1s in an n x n grid, given a list of mines (coordinates where the grid value is 0). A plus sign of order k has a center at (r,c) with four arms of length k-1 extending up, down, left, and right, all consisting of 1s.

The most efficient approach uses dynamic programming. Instead of directly checking for plus signs of different orders, we use a DP table dp to store the maximum length of arms extending from each cell in four directions: left, right, up, and down.

Algorithm:

  1. Initialization: Create a DP table dp of size n x n, initially filled with n. This represents that if there are no mines, the maximum arm length from each cell is n. Then, set dp[x][y] = 0 for each mine location (x,y) from the input mines.

  2. Dynamic Programming: Iterate through the grid. For each cell (i,j), we calculate the maximum arm length extending from that cell in four directions:

    • Left: left is incremented for each consecutive 1 encountered moving left from (i,j). If a 0 is encountered, left is reset to 0.
    • Right: Similar to left, but moving right.
    • Up: Similar to left, but moving up.
    • Down: Similar to left, but moving down.

    After calculating the arm lengths in each direction, the dp[i][j] is updated to be the minimum of these four lengths. This is because the order of the plus sign is limited by the shortest arm.

  3. Find Maximum: Finally, iterate through the DP table and find the maximum value in dp. This maximum value represents the order of the largest plus sign.

Time Complexity: O(n^2), where n is the size of the grid. We iterate through the grid once for initialization and again for the DP calculations.

Space Complexity: O(n^2) to store the DP table.

Code Explanation (Python):

class Solution:
    def orderOfLargestPlusSign(self, n: int, mines: List[List[int]]) -> int:
        dp = [[n] * n for _ in range(n)]  # Initialize DP table
        for x, y in mines:
            dp[x][y] = 0  # Mark mines as 0
 
        for i in range(n):
            left = right = up = down = 0  # Arm lengths for each direction
            for j, k in zip(range(n), reversed(range(n))):  # Iterate left to right and right to left simultaneously
                left = left + 1 if dp[i][j] else 0
                right = right + 1 if dp[i][k] else 0
                up = up + 1 if dp[j][i] else 0
                down = down + 1 if dp[k][i] else 0
                dp[i][j] = min(dp[i][j], left)  # Update dp with min arm length
                dp[i][k] = min(dp[i][k], right)
                dp[j][i] = min(dp[j][i], up)
                dp[k][i] = min(dp[k][i], down)
 
        return max(max(v) for v in dp) # Find the max value in the DP table.

The other languages (Java, C++, Go) follow the same logic with minor syntactic differences. The key is the efficient use of dynamic programming to avoid redundant calculations when checking for plus signs of different orders.