- {x}
- Form Largest Integer With Digits That Add up to Target
- Number of Students Doing Homework at a Given Time
- Rearrange Words in a Sentence
- People Whose List of Favorite Companies Is Not a Subset of Another List
- Maximum Number of Darts Inside of a Circular Dartboard
- Active Users
- Check If a Word Occurs As a Prefix of Any Word in a Sentence
- Maximum Number of Vowels in a Substring of Given Length
- Pseudo-Palindromic Paths in a Binary Tree
- Max Dot Product of Two Subsequences
- Rectangles Area
- Make Two Arrays Equal by Reversing Subarrays
- Check If a String Contains All Binary Codes of Size K
- Course Schedule IV
- Cherry Pickup II
- Maximum Product of Two Elements in an Array
- Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts
- Read More...

Pseudo-Palindromic Paths in a Binary Tree
Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.
Return the number of pseudo-palindromic paths going from the root node to leaf nodes.
Example 1:
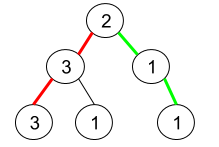
Input: root = [2,3,1,3,1,null,1] Output: 2 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 2:
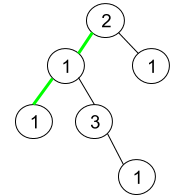
Input: root = [2,1,1,1,3,null,null,null,null,null,1] Output: 1 Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 3:
Input: root = [9] Output: 1
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 9
Solution Explanation: Pseudo-Palindromic Paths in a Binary Tree
This problem asks us to find the number of paths from the root to a leaf node in a binary tree such that the sequence of node values along the path can be rearranged to form a palindrome. A path is considered "pseudo-palindromic" if it meets this condition.
The key insight is that a sequence of numbers can be rearranged to form a palindrome if and only if at most one number appears an odd number of times. We can efficiently track this using bit manipulation.
Approach: Depth-First Search (DFS) with Bit Manipulation
We use a depth-first search (DFS) to traverse the binary tree. For each path, we maintain a bitmask to represent the counts of each digit (1-9).
-
Bitmask: We use a 10-bit integer (since digits are 1-9). The i-th bit is set (1) if the digit
ihas appeared an odd number of times in the current path, and unset (0) otherwise. -
DFS Function: The
dfsfunction recursively explores the tree.- Base Case (Leaf Node): If we reach a leaf node, we check the bitmask:
- If
mask & (mask - 1) == 0, it means at most one bit is set (meaning at most one digit has an odd count), so the path is pseudo-palindromic. We increment the count of pseudo-palindromic paths. - Otherwise, the path is not pseudo-palindromic.
- If
- Recursive Step: For each non-leaf node, we update the bitmask by XORing it with
1 << node.val. XORing toggles the bit corresponding to the current node's value. We recursively calldfson the left and right subtrees, summing the results.
- Base Case (Leaf Node): If we reach a leaf node, we check the bitmask:
Time and Space Complexity Analysis
-
Time Complexity: O(N), where N is the number of nodes in the tree. We visit each node exactly once during the DFS traversal. The bit manipulation operations are constant time.
-
Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack in the DFS. In the worst case (a skewed tree), H could be N.
Code Implementation (Python)
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def pseudoPalindromicPaths(self, root: TreeNode) -> int:
count = 0
def dfs(node: TreeNode, mask: int):
nonlocal count # Access the outer count variable
mask ^= (1 << node.val) # Toggle the bit for the current node's value
if not node.left and not node.right: # Leaf node
if (mask & (mask - 1)) == 0: # Check if at most one bit is set
count += 1
return
if node.left:
dfs(node.left, mask)
if node.right:
dfs(node.right, mask)
if root:
dfs(root, 0) # Start DFS with an empty mask
return countThe code in other languages (Java, C++, Go, TypeScript, Rust) follows the same logic, with the primary differences being syntax and data structure handling. The core algorithm of DFS with bit manipulation remains consistent across all implementations.