- {x}
- Lucky Numbers in a Matrix
- Design a Stack With Increment Operation
- Balance a Binary Search Tree
- Maximum Performance of a Team
- Total Sales Amount by Year
- Find the Distance Value Between Two Arrays
- Cinema Seat Allocation
- Sort Integers by The Power Value
- Pizza With 3n Slices
- Create Target Array in the Given Order
- Four Divisors
- Check if There is a Valid Path in a Grid
- Longest Happy Prefix
- Capital Gain/Loss
- Find Lucky Integer in an Array
- Count Number of Teams
- Design Underground System
- Read More...

Pizza With 3n Slices
There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:
- You will pick any pizza slice.
- Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
- Your friend Bob will pick the next slice in the clockwise direction of your pick.
- Repeat until there are no more slices of pizzas.
Given an integer array slices that represent the sizes of the pizza slices in a clockwise direction, return the maximum possible sum of slice sizes that you can pick.
Example 1:
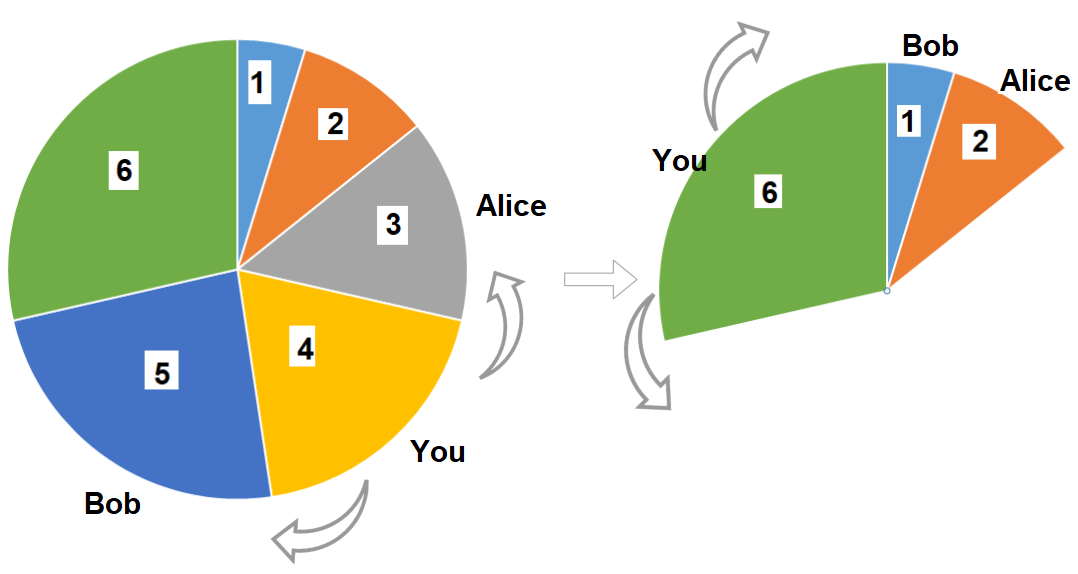
Input: slices = [1,2,3,4,5,6] Output: 10 Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.
Example 2:
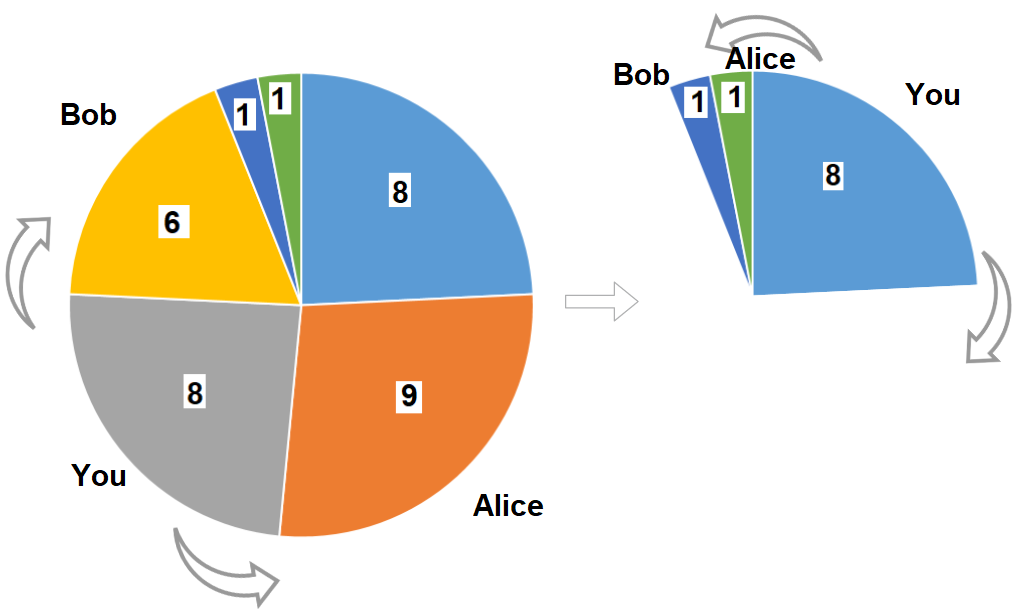
Input: slices = [8,9,8,6,1,1] Output: 16 Explanation: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.
Constraints:
3 * n == slices.length1 <= slices.length <= 5001 <= slices[i] <= 1000
1388. Pizza With 3n Slices
Problem Description
Given a circular pizza with 3n slices of varying sizes, you, Alice, and Bob take turns picking slices. You pick first, then Alice picks the next slice counter-clockwise, and Bob picks the next slice clockwise. This process repeats until all slices are taken. The goal is to maximize the total size of the slices you pick.
Solution: Dynamic Programming
This problem can be elegantly solved using dynamic programming. The key insight is to realize that we can frame the problem as selecting n non-adjacent slices from a circular array of size 3n to maximize the sum.
Approach:
-
Reduce to Subproblems: We divide the circular array into two linear arrays: one excluding the first slice, and another excluding the last slice. We then solve the subproblem of finding the maximum sum of
nnon-adjacent slices within each linear array. The maximum of these two subproblem solutions is the answer. -
Dynamic Programming State: We define
dp[i][j]to represent the maximum sum achievable by selectingjnon-adjacent slices from the firstislices of a linear array. -
Recurrence Relation: The recurrence relation is as follows:
dp[i][j] = max(dp[i-1][j], dp[i-2][j-1] + slices[i-1])
This means we either don't select the
i-th slice (usingdp[i-1][j]), or we select it (addingslices[i-1]and usingdp[i-2][j-1]since we can't select adjacent slices). -
Base Cases:
dp[i][0] = 0for alli(no slices selected).dp[i][j] = -Infinityifj > i(can't select more slices than available).
Code (Python):
def maxSizeSlices(slices):
n = len(slices) // 3
def max_sum(nums):
m = len(nums)
dp = [[float('-inf')] * (n + 1) for _ in range(m + 1)]
for i in range(m + 1):
dp[i][0] = 0
for i in range(1, m + 1):
for j in range(1, min(i, n) + 1):
dp[i][j] = max(dp[i-1][j], (dp[i-2][j-1] if i >= 2 else 0) + nums[i-1])
return dp[m][n]
return max(max_sum(slices[:-1]), max_sum(slices[1:]))
Time Complexity: O(n²) - due to the nested loops in the dynamic programming solution. n is the number of slices you need to pick (which is len(slices) // 3).
Space Complexity: O(n²) - due to the dp table.
Code in other languages (brief structure):
The approach remains the same for other languages; only the syntax and data structure implementations change slightly:
Java:
class Solution {
public int maxSizeSlices(int[] slices) {
int n = slices.length / 3;
// ... (max_sum function implementation similar to Python) ...
return Math.max(max_sum(Arrays.copyOfRange(slices, 0, slices.length - 1)), max_sum(Arrays.copyOfRange(slices, 1, slices.length)));
}
// ... (max_sum function implementation) ...
}C++:
class Solution {
public:
int maxSizeSlices(vector<int>& slices) {
int n = slices.size() / 3;
// ... (max_sum function implementation similar to Python, using vectors) ...
return max(max_sum(vector<int>(slices.begin(), slices.end() - 1)), max_sum(vector<int>(slices.begin() + 1, slices.end())));
}
// ... (max_sum function implementation) ...
};Other languages (Go, Javascript, etc.) would follow a similar pattern. The core logic using dynamic programming to solve the non-adjacent slice selection problem remains consistent.