{x}
blog image

Balance a Binary Search Tree

Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.

A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

 

Example 1:

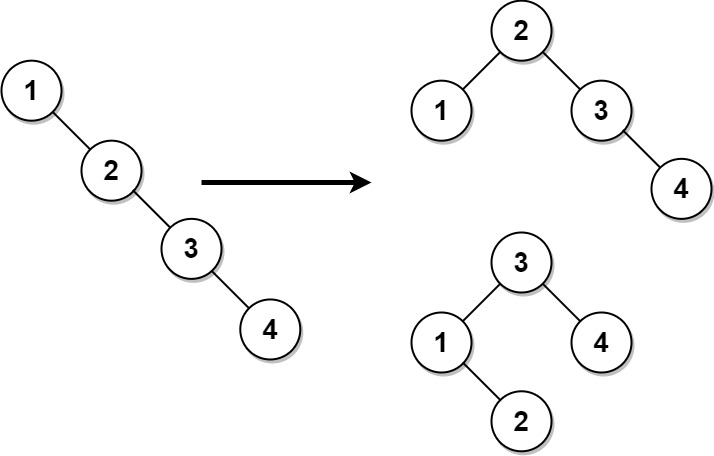
Input: root = [1,null,2,null,3,null,4,null,null]
Output: [2,1,3,null,null,null,4]
Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.

Example 2:

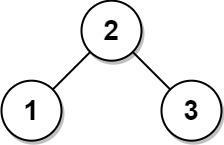
Input: root = [2,1,3]
Output: [2,1,3]

 

Constraints:

  • The number of nodes in the tree is in the range [1, 104].
  • 1 <= Node.val <= 105

Solution Explanation: Balancing a Binary Search Tree

This problem requires transforming a given Binary Search Tree (BST) into a balanced BST while preserving the original node values. The optimal approach involves these steps:

  1. In-order Traversal: Perform an in-order traversal of the input BST. In-order traversal visits nodes in ascending order for a BST. This gives us a sorted array (nums) containing all the node values.

  2. Balanced BST Construction: Construct a new balanced BST from the sorted array using a recursive helper function build(i, j). This function works as follows:

    • Base Case: If i > j (empty subarray), return null (representing an empty subtree).
    • Recursive Step: Find the middle element mid = (i + j) / 2. This middle element becomes the root of the subtree being constructed. Recursively call build to create the left subtree (build(i, mid - 1)) using elements from i to mid - 1 and the right subtree (build(mid + 1, j)) using elements from mid + 1 to j. Finally, construct and return a new tree node with the middle element as the value, and the left and right subtrees.

Time Complexity Analysis:

  • In-order traversal takes O(n) time, where n is the number of nodes.
  • Building the balanced BST also takes O(n) time because each node is visited and processed once during the recursive calls.
  • Therefore, the overall time complexity is O(n).

Space Complexity Analysis:

  • The in-order traversal uses O(h) space in the worst case (a skewed tree) where h is the height of the tree (can be O(n) for a skewed tree, but O(log n) for a balanced tree).
  • The recursive build function uses O(h) space on the call stack, again potentially O(n) for a skewed input tree, but O(log n) for balanced input.
  • The nums array stores n elements, requiring O(n) space.
  • Thus, the overall space complexity is O(n).

Code Examples:

The code examples provided in Python, Java, C++, Go, and TypeScript all follow the same algorithm. They differ only in syntax and data structure implementations. All implementations demonstrate the in-order traversal to create the sorted nums array, followed by the recursive build function to construct the balanced BST.

Example (Python):

class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:
        nums = []
        def inorder(node):
            if node:
                inorder(node.left)
                nums.append(node.val)
                inorder(node.right)
 
        def build(l, r):
            if l > r:
                return None
            mid = (l + r) // 2
            node = TreeNode(nums[mid])
            node.left = build(l, mid - 1)
            node.right = build(mid + 1, r)
            return node
 
        inorder(root)
        return build(0, len(nums) - 1)

The other languages follow a similar structure, adapting the syntax and data types accordingly. The core algorithm remains consistent across all implementations.