{x}
blog image

Operations on Tree

You are given a tree with n nodes numbered from 0 to n - 1 in the form of a parent array parent where parent[i] is the parent of the ith node. The root of the tree is node 0, so parent[0] = -1 since it has no parent. You want to design a data structure that allows users to lock, unlock, and upgrade nodes in the tree.

The data structure should support the following functions:

  • Lock: Locks the given node for the given user and prevents other users from locking the same node. You may only lock a node using this function if the node is unlocked.
  • Unlock: Unlocks the given node for the given user. You may only unlock a node using this function if it is currently locked by the same user.
  • Upgrade: Locks the given node for the given user and unlocks all of its descendants regardless of who locked it. You may only upgrade a node if all 3 conditions are true:
    • The node is unlocked,
    • It has at least one locked descendant (by any user), and
    • It does not have any locked ancestors.

Implement the LockingTree class:

  • LockingTree(int[] parent) initializes the data structure with the parent array.
  • lock(int num, int user) returns true if it is possible for the user with id user to lock the node num, or false otherwise. If it is possible, the node num will become locked by the user with id user.
  • unlock(int num, int user) returns true if it is possible for the user with id user to unlock the node num, or false otherwise. If it is possible, the node num will become unlocked.
  • upgrade(int num, int user) returns true if it is possible for the user with id user to upgrade the node num, or false otherwise. If it is possible, the node num will be upgraded.

 

Example 1:

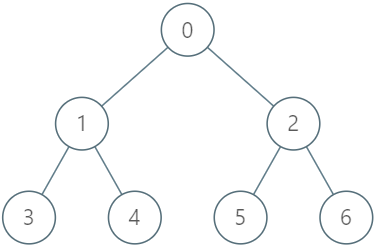
Input
["LockingTree", "lock", "unlock", "unlock", "lock", "upgrade", "lock"]
[[[-1, 0, 0, 1, 1, 2, 2]], [2, 2], [2, 3], [2, 2], [4, 5], [0, 1], [0, 1]]
Output
[null, true, false, true, true, true, false]

Explanation
LockingTree lockingTree = new LockingTree([-1, 0, 0, 1, 1, 2, 2]);
lockingTree.lock(2, 2);    // return true because node 2 is unlocked.
                           // Node 2 will now be locked by user 2.
lockingTree.unlock(2, 3);  // return false because user 3 cannot unlock a node locked by user 2.
lockingTree.unlock(2, 2);  // return true because node 2 was previously locked by user 2.
                           // Node 2 will now be unlocked.
lockingTree.lock(4, 5);    // return true because node 4 is unlocked.
                           // Node 4 will now be locked by user 5.
lockingTree.upgrade(0, 1); // return true because node 0 is unlocked and has at least one locked descendant (node 4).
                           // Node 0 will now be locked by user 1 and node 4 will now be unlocked.
lockingTree.lock(0, 1);    // return false because node 0 is already locked.

 

Constraints:

  • n == parent.length
  • 2 <= n <= 2000
  • 0 <= parent[i] <= n - 1 for i != 0
  • parent[0] == -1
  • 0 <= num <= n - 1
  • 1 <= user <= 104
  • parent represents a valid tree.
  • At most 2000 calls in total will be made to lock, unlock, and upgrade.

Solution Explanation:

This problem involves designing a LockingTree data structure that manages locking and unlocking of nodes in a tree. The tree is represented using a parent array, where parent[i] indicates the parent of node i. The root node is node 0, with parent[0] = -1.

The data structure supports three operations:

  1. lock(num, user): Locks node num for user user. Returns true if successful (node was unlocked), false otherwise.

  2. unlock(num, user): Unlocks node num for user user. Returns true if successful (node was locked by user), false otherwise.

  3. upgrade(num, user): Upgrades node num for user user. This locks node num for user user and unlocks all its descendants, regardless of who locked them. The upgrade is only possible if:

    • Node num is unlocked.
    • Node num has at least one locked descendant.
    • Node num has no locked ancestors.

Approach:

The solution uses a combination of arrays and potentially lists (depending on the language) to efficiently manage the tree structure and locking information.

  1. Data Structures:

    • locked: An array to store the user ID locking each node. -1 indicates the node is unlocked.
    • parent: The input parent array representing the tree structure.
    • children: A list/array of lists/arrays to represent the children of each node. This is built from the parent array for efficient traversal.

  2. lock and unlock: These operations are straightforward. Check the locked array to see if the node is already locked or if the unlocking user matches the locking user.

  3. upgrade: This is the most complex operation. It involves three checks:

    • Ancestor check: Iterate up the tree from the target node to check for locked ancestors using the parent array. If any ancestor is locked, the upgrade fails.
    • Descendant check: Perform a Depth-First Search (DFS) on the descendants of the target node. This recursively checks if any descendant is locked. If a locked descendant is found, unlock it and set a find flag to true.
    • Upgrade if possible: If both checks pass (no locked ancestors and at least one locked descendant), lock the target node for the specified user and return true.

Time and Space Complexity:

  • Time Complexity:

    • lock and unlock: O(1)
    • upgrade: O(N) in the worst case, where N is the number of nodes in the tree, due to the traversal of ancestors and descendants.

  • Space Complexity:

    • O(N) to store the locked, parent, and children arrays/lists. The recursive DFS call stack in upgrade also contributes to this space complexity.

Code Explanation (Python Example):

The Python code provided implements this approach efficiently. The __init__ method builds the children array from the parent array. The lock, unlock, and upgrade methods implement the logic described above. The dfs function in upgrade performs the Depth-First Search to check for and unlock locked descendants.

The other language implementations follow the same underlying logic, with minor syntactic differences due to the language specifics. Each language version is structured similarly to optimize the operations and ensure efficient tree traversal.