{x}
blog image

Number Of Ways To Reconstruct A Tree

You are given an array pairs, where pairs[i] = [xi, yi], and:

  • There are no duplicates.
  • xi < yi

Let ways be the number of rooted trees that satisfy the following conditions:

  • The tree consists of nodes whose values appeared in pairs.
  • A pair [xi, yi] exists in pairs if and only if xi is an ancestor of yi or yi is an ancestor of xi.
  • Note: the tree does not have to be a binary tree.

Two ways are considered to be different if there is at least one node that has different parents in both ways.

Return:

  • 0 if ways == 0
  • 1 if ways == 1
  • 2 if ways > 1

A rooted tree is a tree that has a single root node, and all edges are oriented to be outgoing from the root.

An ancestor of a node is any node on the path from the root to that node (excluding the node itself). The root has no ancestors.

 

Example 1:

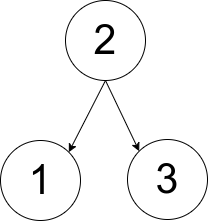
Input: pairs = [[1,2],[2,3]]
Output: 1
Explanation: There is exactly one valid rooted tree, which is shown in the above figure.

Example 2:

Input: pairs = [[1,2],[2,3],[1,3]]
Output: 2
Explanation: There are multiple valid rooted trees. Three of them are shown in the above figures.

Example 3:

Input: pairs = [[1,2],[2,3],[2,4],[1,5]]
Output: 0
Explanation: There are no valid rooted trees.

 

Constraints:

  • 1 <= pairs.length <= 105
  • 1 <= xi < yi <= 500
  • The elements in pairs are unique.

Solution Explanation

This problem asks to determine the number of ways to reconstruct a rooted tree from a given set of pairs, where each pair represents two nodes that are ancestors of each other. The solution involves graph theory and topological sorting concepts.

The core idea is to build an adjacency matrix representing the relationships between nodes. Then, we iterate through the nodes, checking for consistency and the number of possible roots.

Algorithm:

  1. Build Adjacency Matrix and Degree List: Create an adjacency matrix g where g[i][j] = true if node i and node j are connected (ancestor-descendant). Simultaneously, create a list v to store the degree (number of neighbors) for each node.

  2. Find Nodes: Extract all nodes present in the pairs.

  3. Topological Sort (Implicit): The code implicitly performs a topological sort by sorting nodes based on their degree (number of neighbors). Nodes with fewer neighbors are processed first. This helps determine potential roots and check for inconsistencies early.

  4. Check for Root and Consistency: The main loop iterates through the sorted nodes. For each node x, it finds the next node y connected to it.

    • Inconsistency Check: If a node x is connected to y, it verifies that all neighbors of x are also connected to y. If not, it means there's no valid tree, returning 0.
    • Root Count: If a node x doesn't have any connected node y after it, it's a potential root. The count of such nodes(root) is tracked.
    • Multiple Roots: If root > 1, it indicates multiple potential roots, making the reconstruction impossible, so it returns 0.
    • Equal Degree Check: If two nodes x and y have equal degrees, it means there might be multiple ways to construct the tree (more than one valid root). This condition sets equal to true.

  5. Return the Result:

    • If root > 1 (more than one root): Return 0
    • If equal (multiple ways to construct the tree due to equally sized subtrees): Return 2
    • Otherwise (exactly one way): Return 1

Time Complexity Analysis:

  • Building the adjacency matrix and degree list takes O(P), where P is the number of pairs.
  • Sorting the nodes takes O(N log N), where N is the number of nodes.
  • Iterating through the nodes and checking for consistency takes O(N * D), where D is the maximum degree of a node. In the worst case, D could be approximately N, so this part is O(N^2).

Therefore, the overall time complexity is dominated by the sorting and consistency check, resulting in O(N^2). In practice, because the number of nodes is limited (<=500), the quadratic complexity is acceptable.

Space Complexity Analysis:

The space complexity is dominated by the adjacency matrix g, which requires O(N^2) space. The degree list v and the list of nodes also require O(N) space. Thus, the overall space complexity is O(N^2).

The provided code in Python, Java, C++, and Go implements this algorithm efficiently. The use of adjacency matrix makes the consistency check quite straightforward. The sorting step ensures that we can detect and handle inconsistencies and multiple roots efficiently.