- {x}
- Minimum Time Difference
- Single Element in a Sorted Array
- Reverse String II
- 01 Matrix
- Diameter of Binary Tree
- Output Contest Matches
- Boundary of Binary Tree
- Remove Boxes
- Number of Provinces
- Split Array with Equal Sum
- Binary Tree Longest Consecutive Sequence II
- Game Play Analysis IV
- Student Attendance Record I
- Student Attendance Record II
- Optimal Division
- Brick Wall
- Split Concatenated Strings
- Read More...

Number of Provinces
There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.
A province is a group of directly or indirectly connected cities and no other cities outside of the group.
You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.
Return the total number of provinces.
Example 1:
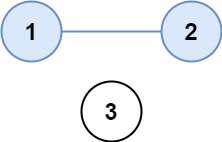
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]] Output: 2
Example 2:
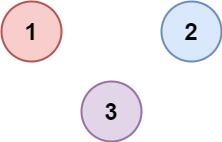
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]] Output: 3
Constraints:
1 <= n <= 200n == isConnected.lengthn == isConnected[i].lengthisConnected[i][j]is1or0.isConnected[i][i] == 1isConnected[i][j] == isConnected[j][i]
547. Number of Provinces
Description
The problem asks to find the number of provinces in a given graph represented by an adjacency matrix isConnected. A province is a group of directly or indirectly connected cities. Two cities are directly connected if isConnected[i][j] == 1.
Solutions
Two common approaches to solve this problem are Depth-First Search (DFS) and Union-Find.
Solution 1: Depth-First Search (DFS)
This approach uses DFS to traverse the graph and identify connected components.
Algorithm:
-
Initialization: Create a boolean array
visof sizen(number of cities), initialized tofalse. This array tracks visited cities. Initialize a counteransto 0, representing the number of provinces. -
Iteration: Iterate through each city
ifrom 0 ton-1. -
DFS Check: If
vis[i]isfalse(cityiis not visited), it means a new province is found. Incrementans. Call a recursive DFS function starting from cityi. -
DFS Function: The DFS function
dfs(i)marksvis[i]astrue. Then, it iterates through the neighbors of cityi(citiesjwhereisConnected[i][j] == 1). If a neighborjis not visited (vis[j]isfalse), it recursively callsdfs(j)to explore that neighbor's connected components.
Time Complexity: O(N^2), where N is the number of cities. This is because we visit each city and its neighbors once. In the worst case, we might traverse all the edges of the graph.
Space Complexity: O(N) to store the vis array. The recursive call stack in DFS also contributes to space complexity, but it's bounded by the height of the graph, which is at most N in this case.
Code (Python):
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
n = len(isConnected)
vis = [False] * n
ans = 0
def dfs(i: int):
vis[i] = True
for j in range(n):
if isConnected[i][j] and not vis[j]:
dfs(j)
for i in range(n):
if not vis[i]:
dfs(i)
ans += 1
return ans
Similar code can be written in other languages like Java, C++, JavaScript, etc., following the same algorithm.
Solution 2: Union-Find
Union-find is a disjoint-set data structure that efficiently tracks connected components.
Algorithm:
-
Initialization: Create a parent array
pof sizen, where initiallyp[i] = i(each city is its own parent, representing separate components). Initialize a countanston(initially, each city is a separate province). -
Iteration: Iterate through the
isConnectedmatrix. -
Union: If
isConnected[i][j] == 1, find the root parents ofiandjusing afindfunction (with path compression for optimization). If the roots are different, it meansiandjbelong to different components. Perform a union operation by settingp[root_of_i] = root_of_j, merging the components. Decrementansbecause we've merged two provinces. -
Find Function: The
findfunction recursively finds the root parent of a node, applying path compression to optimize subsequentfindoperations.
Time Complexity: O(N^2 * α(N)), where α(N) is the inverse Ackermann function, which grows extremely slowly and is practically a constant. The O(N^2) factor comes from iterating through the adjacency matrix. Path compression significantly improves the performance of Union-Find.
Space Complexity: O(N) to store the p array.
Code (Python):
class Solution:
def findCircleNum(self, isConnected: List[List[int]]) -> int:
n = len(isConnected)
p = list(range(n))
ans = n
def find(x: int) -> int:
if p[x] != x:
p[x] = find(p[x]) # Path compression
return p[x]
for i in range(n):
for j in range(i + 1, n):
if isConnected[i][j]:
root_i = find(i)
root_j = find(j)
if root_i != root_j:
p[root_i] = root_j
ans -= 1
return ansAgain, similar code can be written in other languages.
Choosing between DFS and Union-Find:
For this specific problem, DFS is often slightly simpler to implement. Union-Find's advantage becomes more apparent in problems involving more complex queries on connected components. The asymptotic time complexities are similar in practice, with Union-Find possibly having a slight edge due to path compression.