{x}
blog image

Minimum Number of Taps to Open to Water a Garden

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e., the length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

 

Example 1:

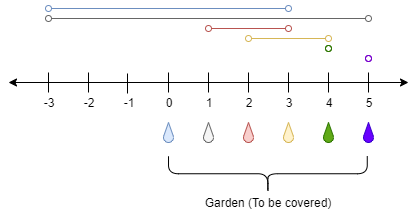
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

 

Constraints:

  • 1 <= n <= 104
  • ranges.length == n + 1
  • 0 <= ranges[i] <= 100

1326. Minimum Number of Taps to Open to Water a Garden

Problem Description

Given a garden of length n and an array ranges where ranges[i] represents the range of the i-th tap, find the minimum number of taps needed to water the entire garden. Each tap at index i can water the interval [i - ranges[i], i + ranges[i]]. If it's impossible to water the entire garden, return -1.

Solution: Greedy Approach

The optimal solution involves a greedy strategy. We prioritize taps that cover the most ground. The algorithm works as follows:

  1. Preprocessing: Create an array last where last[i] stores the farthest right endpoint reachable starting from position i. This is done by iterating through the ranges array and updating last accordingly. For each tap, we calculate its left and right coverage and update last to record the maximum right reach starting from that left point.

  2. Greedy Iteration: We iterate from left to right through the garden (0 to n). We maintain:

    • ans: The count of taps used.
    • mx: The farthest right point currently reachable.
    • pre: The farthest right point reached by the previously used tap.

  3. Iteration Logic:

    • In each iteration, mx is updated to the maximum reachable point from the current position (i).
    • If mx is less than or equal to i, it means we're stuck and cannot reach further; thus, the garden cannot be fully watered, so we return -1.
    • If pre equals i, this means we need to use a new tap to extend our reach. We increment ans and update pre to the new maximum reachable point (mx).

  4. Return Value: After the loop completes, ans represents the minimum number of taps required.

Time and Space Complexity

  • Time Complexity: O(n), where n is the length of the garden. The preprocessing and iteration both take linear time.
  • Space Complexity: O(n) to store the last array.

Code Implementation (Python)

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        last = [0] * (n + 1)
        for i, x in enumerate(ranges):
            l, r = max(0, i - x), i + x  # Calculate left and right coverage
            last[l] = max(last[l], r)     # Update last[l] with max reach from l
 
        ans = mx = pre = 0
        for i in range(n):
            mx = max(mx, last[i])         # Update max reach
            if mx <= i: return -1         # Cannot proceed further
            if pre == i:                  # Need a new tap
                ans += 1
                pre = mx                  # Update previous reach
        return ans

Note: The code in other languages (Java, C++, Go, TypeScript, Rust) provided in the original response follows the same algorithm with minor syntactic variations for each language. The core logic remains consistent across all implementations.