{x}
blog image

Maximum Points in an Archery Competition

Alice and Bob are opponents in an archery competition. The competition has set the following rules:

  1. Alice first shoots numArrows arrows and then Bob shoots numArrows arrows.
  2. The points are then calculated as follows:
    1. The target has integer scoring sections ranging from 0 to 11 inclusive.
    2. For each section of the target with score k (in between 0 to 11), say Alice and Bob have shot ak and bk arrows on that section respectively. If ak >= bk, then Alice takes k points. If ak < bk, then Bob takes k points.
    3. However, if ak == bk == 0, then nobody takes k points.

  • For example, if Alice and Bob both shot 2 arrows on the section with score 11, then Alice takes 11 points. On the other hand, if Alice shot 0 arrows on the section with score 11 and Bob shot 2 arrows on that same section, then Bob takes 11 points.

You are given the integer numArrows and an integer array aliceArrows of size 12, which represents the number of arrows Alice shot on each scoring section from 0 to 11. Now, Bob wants to maximize the total number of points he can obtain.

Return the array bobArrows which represents the number of arrows Bob shot on each scoring section from 0 to 11. The sum of the values in bobArrows should equal numArrows.

If there are multiple ways for Bob to earn the maximum total points, return any one of them.

 

Example 1:

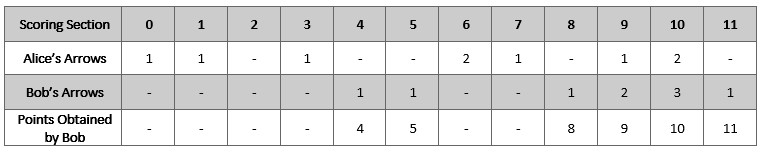
Input: numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
Output: [0,0,0,0,1,1,0,0,1,2,3,1]
Explanation: The table above shows how the competition is scored. 
Bob earns a total point of 4 + 5 + 8 + 9 + 10 + 11 = 47.
It can be shown that Bob cannot obtain a score higher than 47 points.

Example 2:

Input: numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
Output: [0,0,0,0,0,0,0,0,1,1,1,0]
Explanation: The table above shows how the competition is scored.
Bob earns a total point of 8 + 9 + 10 = 27.
It can be shown that Bob cannot obtain a score higher than 27 points.

 

Constraints:

  • 1 <= numArrows <= 105
  • aliceArrows.length == bobArrows.length == 12
  • 0 <= aliceArrows[i], bobArrows[i] <= numArrows
  • sum(aliceArrows[i]) == numArrows

Solution Explanation

This problem asks to find the optimal allocation of numArrows arrows for Bob to maximize his score against Alice, given Alice's arrow allocation aliceArrows. The solution utilizes bit manipulation and a greedy approach to efficiently explore the possibilities.

Approach

  1. Bitmasking: We iterate through all possible subsets of the 12 scoring sections (0 to 11) using bit manipulation. Each bit in the mask represents a section: 1 means Bob shoots an arrow in that section, and 0 means he doesn't.

  2. Greedy Strategy: For each mask, we determine Bob's arrow allocation greedily. For each section i where the mask has a 1, Bob shoots aliceArrows[i] + 1 arrows to guarantee he wins that section.

  3. Remaining Arrows: After allocating arrows to winning sections, any remaining arrows (numArrows) are added to section 0. This is a greedy choice, as section 0 contributes the least points.

  4. Score Calculation: Bob's points are calculated by summing the values of the sections he wins (sections with a 1 in the mask).

  5. Maximization: We keep track of the mask that yields the maximum points for Bob.

  6. Result: Finally, we construct and return bobArrows based on the optimal mask.

Time Complexity Analysis

The dominant factor is the iteration over all possible subsets (212 = 4096) using the bitmask. All other operations (allocating arrows, calculating points, etc.) take constant time per subset. Therefore, the time complexity is O(2n), where n is the number of scoring sections (12 in this case).

Space Complexity Analysis

The space complexity is O(n) to store aliceArrows, bobArrows, and other intermediate variables. The space used by the bitmask is constant.

Code Explanation (Python)

The Python code efficiently implements this approach:

class Solution:
    def maximumBobPoints(self, numArrows: int, aliceArrows: List[int]) -> List[int]:
        n = len(aliceArrows)
        best_mask = 0
        max_points = -1
 
        for mask in range(1 << n):  # Iterate through all subsets
            bob_arrows = [0] * n
            points = 0
            arrows_used = 0
 
            for i in range(n):
                if (mask >> i) & 1:  # Check if Bob shoots in section i
                    arrows_needed = aliceArrows[i] + 1
                    arrows_used += arrows_needed
                    bob_arrows[i] = arrows_needed
                    points += i
 
            if arrows_used <= numArrows:  # Check if Bob has enough arrows
                bob_arrows[0] += numArrows - arrows_used  # Assign remaining arrows to section 0
                if points > max_points:
                    max_points = points
                    best_mask = mask
 
        bob_arrows = [0] * n
        arrows_used = 0
        for i in range(n):
            if (best_mask >> i) & 1:
                arrows_needed = aliceArrows[i] + 1
                bob_arrows[i] = arrows_needed
                arrows_used += arrows_needed
        bob_arrows[0] += numArrows - arrows_used
        return bob_arrows

The other language implementations follow a similar structure, adapting the syntax and data structures accordingly. The core logic of bitmasking and greedy allocation remains consistent across all implementations.