- {x}
- Champagne Tower
- Similar RGB Color
- Minimum Swaps To Make Sequences Increasing
- Find Eventual Safe States
- Bricks Falling When Hit
- Unique Morse Code Words
- Split Array With Same Average
- Number of Lines To Write String
- Max Increase to Keep City Skyline
- Soup Servings
- Expressive Words
- Chalkboard XOR Game
- Subdomain Visit Count
- Largest Triangle Area
- Largest Sum of Averages
- Binary Tree Pruning
- Bus Routes
- Read More...

Max Increase to Keep City Skyline
There is a city composed of n x n blocks, where each block contains a single building shaped like a vertical square prism. You are given a 0-indexed n x n integer matrix grid where grid[r][c] represents the height of the building located in the block at row r and column c.
A city's skyline is the outer contour formed by all the building when viewing the side of the city from a distance. The skyline from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of any number of buildings by any amount (the amount can be different per building). The height of a 0-height building can also be increased. However, increasing the height of a building should not affect the city's skyline from any cardinal direction.
Return the maximum total sum that the height of the buildings can be increased by without changing the city's skyline from any cardinal direction.
Example 1:
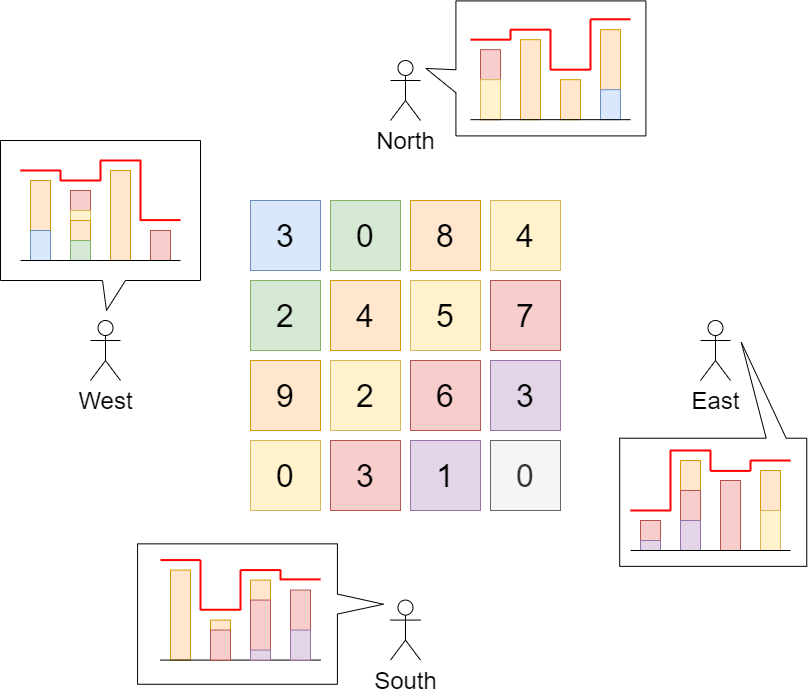
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation: The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]
Example 2:
Input: grid = [[0,0,0],[0,0,0],[0,0,0]] Output: 0 Explanation: Increasing the height of any building will result in the skyline changing.
Constraints:
n == grid.lengthn == grid[r].length2 <= n <= 500 <= grid[r][c] <= 100
Solution Explanation: 807. Max Increase to Keep City Skyline
This problem asks to find the maximum total sum of height increases for buildings in an n x n grid without changing the skyline from any direction (north, east, south, west). The skyline is determined by the maximum height in each row and column.
Approach: A greedy approach is optimal here. The key insight is that for each building, the maximum possible increase in height is limited by the maximum height in its row and the maximum height in its column. We can't increase a building's height beyond either of these constraints without altering the skyline.
Algorithm:
-
Find Row and Column Maximums: Iterate through the grid to find the maximum height in each row and each column. Store these maximums in separate arrays (
rowMaxandcolMax). -
Calculate Maximum Increase for Each Building: For each building
grid[i][j], calculate the maximum possible increase:min(rowMax[i], colMax[j]) - grid[i][j]. This represents how much the building's height can be increased without affecting the skyline. -
Sum the Increases: Sum up the maximum possible increases for all buildings to get the final answer.
Time Complexity Analysis:
- Finding row and column maximums: O(n²) - We iterate through the n x n grid once.
- Calculating maximum increases and summing them: O(n²) - We iterate through the grid again.
Therefore, the overall time complexity is O(n²).
Space Complexity Analysis:
We use two arrays, rowMax and colMax, each of size n to store the maximum heights. The space complexity is thus O(n).
Code Examples (with detailed explanations):
Python:
class Solution:
def maxIncreaseKeepingSkyline(self, grid: List[List[int]]) -> int:
n = len(grid) # Get the size of the grid (assuming it's square)
row_max = [max(row) for row in grid] #List Comprehension for row max
col_max = [max(col) for col in zip(*grid)] #zip(*grid) transposes the grid for column max
total_increase = 0
for i in range(n):
for j in range(n):
max_increase = min(row_max[i], col_max[j]) - grid[i][j] #Find max increase for current building
total_increase += max_increase #Add to total
return total_increase
Java:
class Solution {
public int maxIncreaseKeepingSkyline(int[][] grid) {
int n = grid.length;
int[] rowMax = new int[n];
int[] colMax = new int[n];
// Find row and column maximums
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
rowMax[i] = Math.max(rowMax[i], grid[i][j]);
colMax[j] = Math.max(colMax[j], grid[i][j]);
}
}
int totalIncrease = 0;
// Calculate and sum increases
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
totalIncrease += Math.min(rowMax[i], colMax[j]) - grid[i][j];
}
}
return totalIncrease;
}
}The C++, Go, and TypeScript code would follow a very similar structure to the Python and Java examples, just with different syntax. The core logic remains the same. The key is understanding the greedy approach and how to efficiently find the row and column maximums.