{x}
blog image

Logical OR of Two Binary Grids Represented as Quad-Trees

A Binary Matrix is a matrix in which all the elements are either 0 or 1.

Given quadTree1 and quadTree2. quadTree1 represents a n * n binary matrix and quadTree2 represents another n * n binary matrix.

Return a Quad-Tree representing the n * n binary matrix which is the result of logical bitwise OR of the two binary matrixes represented by quadTree1 and quadTree2.

Notice that you can assign the value of a node to True or False when isLeaf is False, and both are accepted in the answer.

A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:

  • val: True if the node represents a grid of 1's or False if the node represents a grid of 0's.
  • isLeaf: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

We can construct a Quad-Tree from a two-dimensional area using the following steps:

  1. If the current grid has the same value (i.e all 1's or all 0's) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
  2. If the current grid has different values, set isLeaf to False and set val to any value and divide the current grid into four sub-grids as shown in the photo.
  3. Recurse for each of the children with the proper sub-grid.

If you want to know more about the Quad-Tree, you can refer to the wiki.

Quad-Tree format:

The input/output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.

It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].

If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.

 

Example 1:

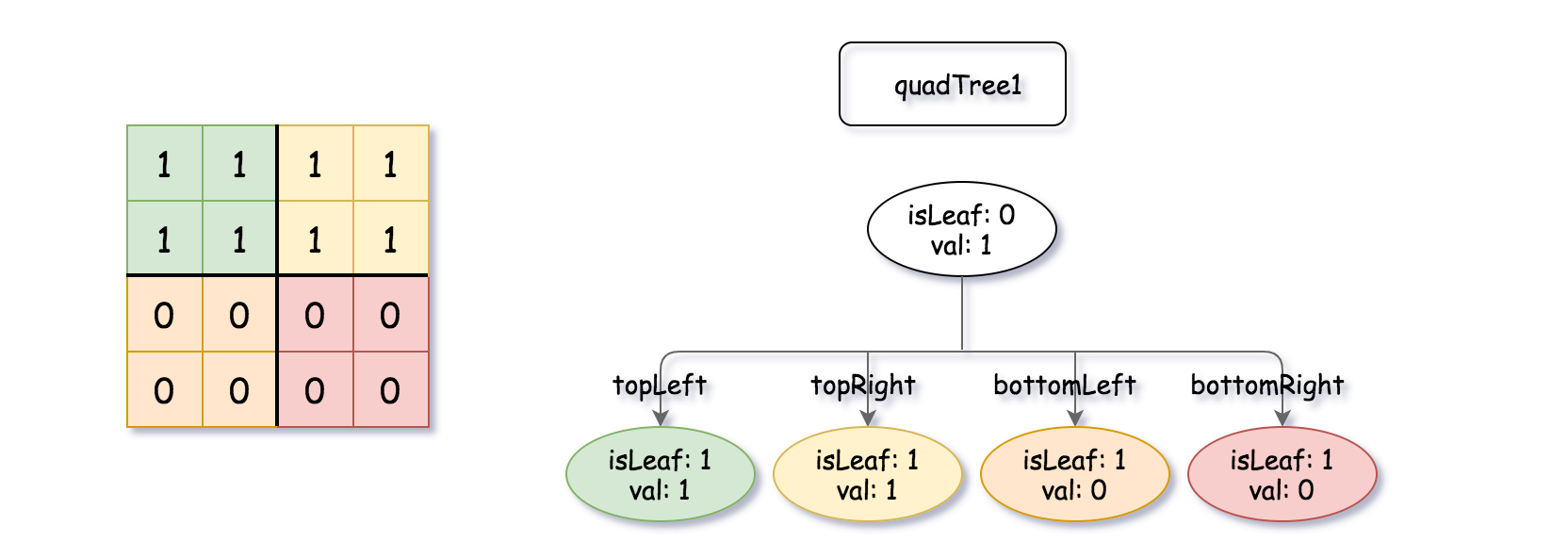
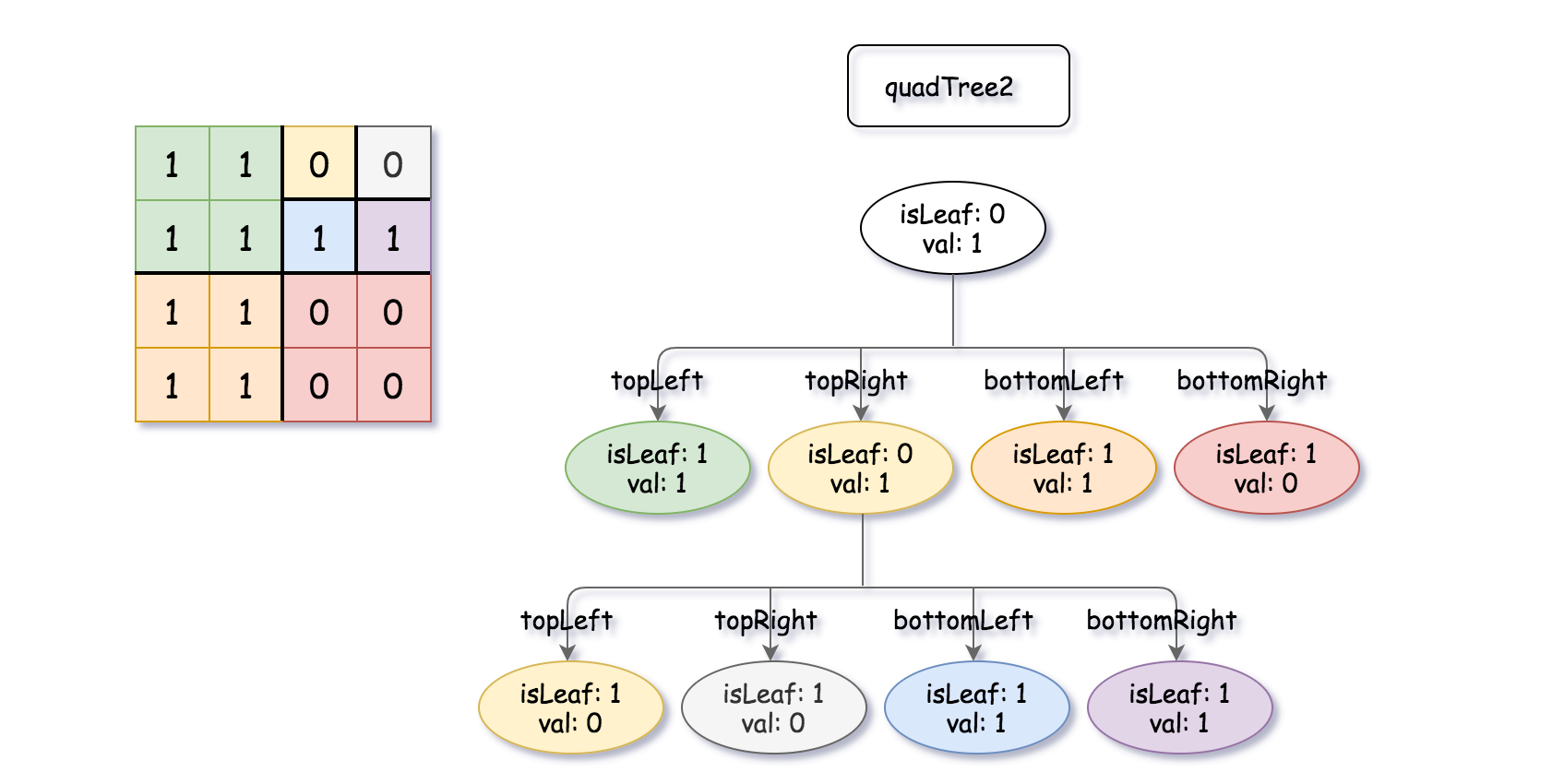
Input: quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
Output: [[0,0],[1,1],[1,1],[1,1],[1,0]]
Explanation: quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.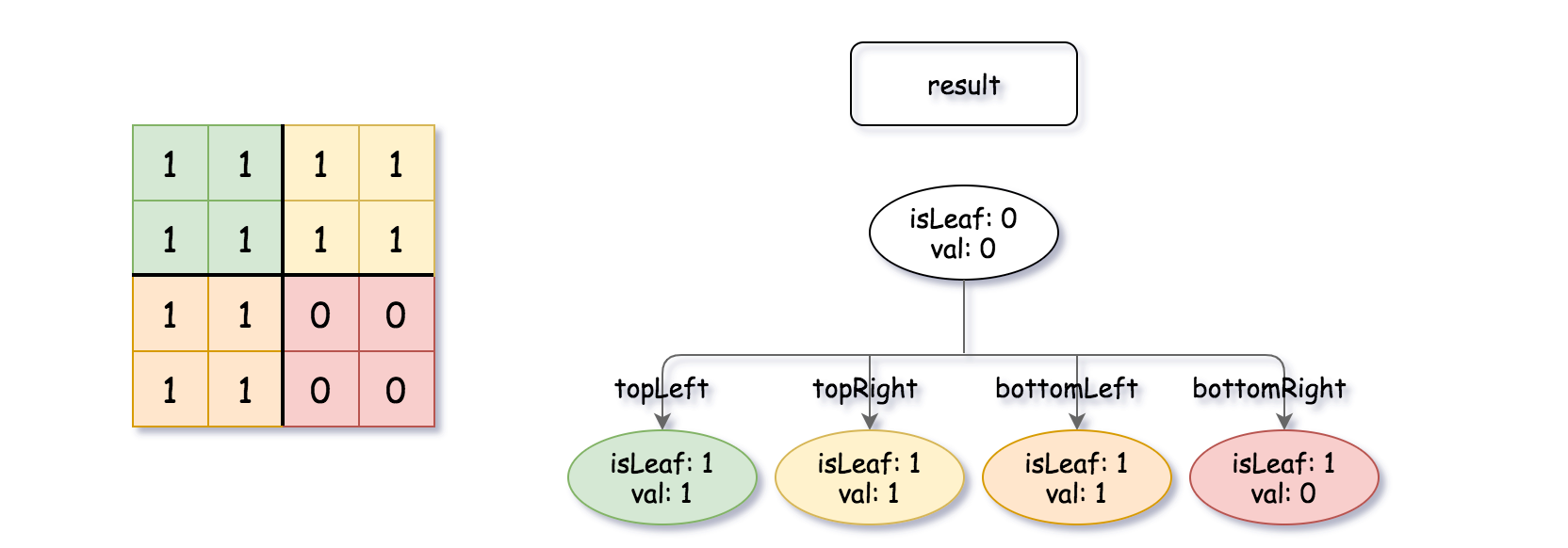

Example 2:

Input: quadTree1 = [[1,0]], quadTree2 = [[1,0]]
Output: [[1,0]]
Explanation: Each tree represents a binary matrix of size 1*1. Each matrix contains only zero.
The resulting matrix is of size 1*1 with also zero.

 

Constraints:

  • quadTree1 and quadTree2 are both valid Quad-Trees each representing a n * n grid.
  • n == 2x where 0 <= x <= 9.

Solution Explanation

This problem involves manipulating QuadTrees, a tree data structure where each node represents a quadrant of a grid. The goal is to compute the bitwise OR of two QuadTrees, resulting in a new QuadTree representing the OR'ed grid.

The solution uses a recursive depth-first search (DFS) approach. The core logic lies within the dfs function (named differently across languages but functionally identical).

Approach:

  1. Base Cases:

    • If both input QuadTree nodes (t1 and t2) are leaf nodes, the result is a new leaf node with its val set to the bitwise OR of t1.val and t2.val.
    • If one node is a leaf node and the other isn't, the result depends on the leaf node's value. If the leaf node's value is True, it's returned directly; otherwise, the non-leaf node is returned. This is because True (1) dominates in the OR operation.

  2. Recursive Step:

    • If neither node is a leaf, a new Node (res) is created.
    • The dfs function is recursively called on each corresponding quadrant (topLeft, topRight, bottomLeft, bottomRight) of t1 and t2, assigning the results to the respective children of res.
    • After the recursive calls, the algorithm checks if the resulting quadrants (res.topLeft, res.topRight, etc.) are all leaf nodes with the same value. If they are, this indicates the entire resulting quadrant can be simplified to a single leaf node. In this case, res is updated to point to one of the leaf nodes.

  3. Return Value:

    • The dfs function returns the res node, representing the resulting QuadTree for the given input sub-quadrants.

Time Complexity Analysis:

The time complexity is O(N), where N is the total number of nodes in the QuadTrees. In the worst-case scenario, where the QuadTrees are not simplified (i.e., they are completely filled), the algorithm visits each node once. The recursive nature of the DFS ensures that every node is processed only once.

Space Complexity Analysis:

The space complexity is O(log N) in the best-case scenario (highly simplified QuadTrees) and O(N) in the worst-case (completely filled QuadTrees). This is due to the recursion stack, which in the worst case holds a maximum depth equal to the height of the QuadTree, which is proportional to log N for balanced trees. In the worst case (completely filled), the recursion stack can grow to the number of nodes in the tree.

The provided code in Python, Java, C++, and Go implements this approach effectively. The slight variations in syntax are due to the differences in the respective languages but the core recursive logic remains consistent.