- {x}
- Split Concatenated Strings
- Next Greater Element III
- Reverse Words in a String III
- Logical OR of Two Binary Grids Represented as Quad-Trees
- Maximum Depth of N-ary Tree
- Subarray Sum Equals K
- Array Partition
- Longest Line of Consecutive One in Matrix
- Binary Tree Tilt
- Find the Closest Palindrome
- Array Nesting
- Reshape the Matrix
- Permutation in String
- Maximum Vacation Days
- Median Employee Salary
- Managers with at Least 5 Direct Reports
- Find Median Given Frequency of Numbers
- Read More...

Binary Tree Tilt
Given the root of a binary tree, return the sum of every tree node's tilt.
The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.
Example 1:
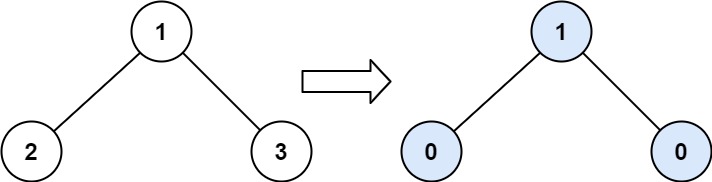
Input: root = [1,2,3] Output: 1 Explanation: Tilt of node 2 : |0-0| = 0 (no children) Tilt of node 3 : |0-0| = 0 (no children) Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3) Sum of every tilt : 0 + 0 + 1 = 1
Example 2:
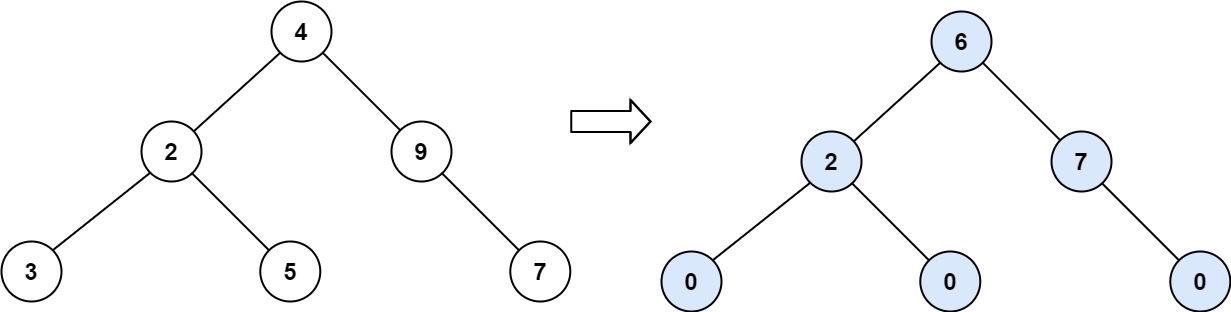
Input: root = [4,2,9,3,5,null,7] Output: 15 Explanation: Tilt of node 3 : |0-0| = 0 (no children) Tilt of node 5 : |0-0| = 0 (no children) Tilt of node 7 : |0-0| = 0 (no children) Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5) Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7) Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16) Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
Example 3:
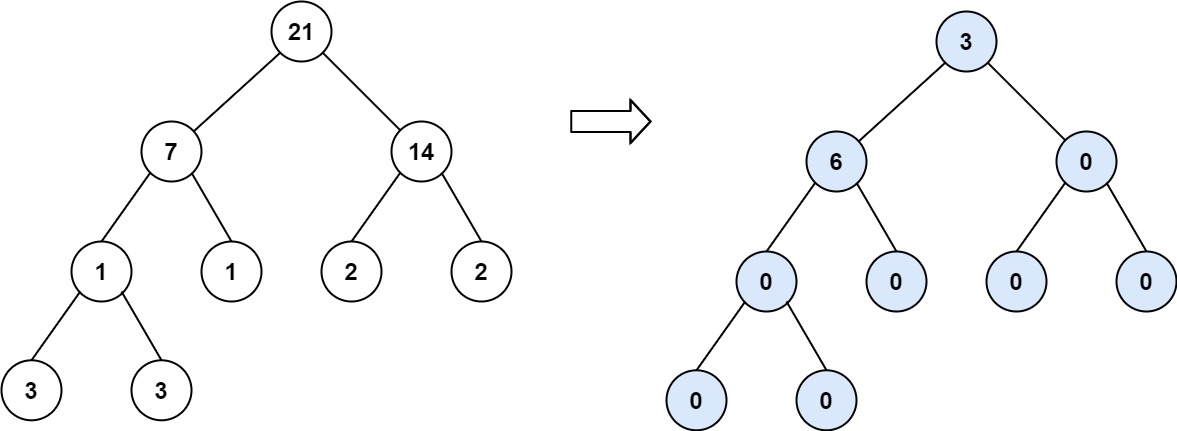
Input: root = [21,7,14,1,1,2,2,3,3] Output: 9
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -1000 <= Node.val <= 1000
Solution Explanation: Binary Tree Tilt
The problem asks to calculate the sum of tilts for all nodes in a binary tree. The tilt of a node is the absolute difference between the sum of its left subtree's node values and the sum of its right subtree's node values.
Approach:
The most efficient approach uses a Depth-First Search (DFS) recursive strategy. A helper function dfs is created to recursively traverse the tree and calculate the tilt at each node.
Algorithm:
-
Base Case: If the current node is
null, the sum of its subtree is 0. Return 0. -
Recursive Calls: Recursively call
dfson the left and right subtrees to get their respective subtree sums (landr). -
Tilt Calculation: Calculate the absolute difference between
landr(abs(l - r)). Add this tilt to a global variableans(which accumulates the total tilt). -
Return Value: Return the sum of the current node's value and the subtree sums (
l + r + root.val). This value is passed up the recursion to the parent node.
Time and Space Complexity:
- Time Complexity: O(N), where N is the number of nodes in the tree. We visit each node exactly once.
- Space Complexity: O(H), where H is the height of the tree. This is due to the recursive call stack. In the worst case (a skewed tree), H can be equal to N. In the best case (a balanced tree), H is log₂(N).
Code Implementation (Python):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findTilt(self, root: Optional[TreeNode]) -> int:
ans = 0 # Global variable to store the total tilt
def dfs(root: Optional[TreeNode]) -> int:
if not root: # Base case: empty subtree
return 0
left_sum = dfs(root.left)
right_sum = dfs(root.right)
nonlocal ans # Access and modify the global variable
ans += abs(left_sum - right_sum)
return left_sum + right_sum + root.val
dfs(root)
return ansThe other language implementations (Java, C++, Go, TypeScript) follow the same algorithmic structure; only the syntax differs. The nonlocal ans in Python is needed to modify the global ans within the nested dfs function. Other languages achieve this using class member variables or similar mechanisms.