{x}
blog image

Get Watched Videos by Your Friends

There are n people, each person has a unique id between 0 and n-1. Given the arrays watchedVideos and friends, where watchedVideos[i] and friends[i] contain the list of watched videos and the list of friends respectively for the person with id = i.

Level 1 of videos are all watched videos by your friends, level 2 of videos are all watched videos by the friends of your friends and so on. In general, the level k of videos are all watched videos by people with the shortest path exactly equal to k with you. Given your id and the level of videos, return the list of videos ordered by their frequencies (increasing). For videos with the same frequency order them alphabetically from least to greatest. 

 

Example 1:

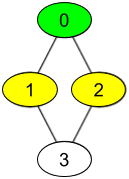
Input: watchedVideos = [["A","B"],["C"],["B","C"],["D"]], friends = [[1,2],[0,3],[0,3],[1,2]], id = 0, level = 1
Output: ["B","C"] 
Explanation: 
You have id = 0 (green color in the figure) and your friends are (yellow color in the figure):
Person with id = 1 -> watchedVideos = ["C"] 
Person with id = 2 -> watchedVideos = ["B","C"] 
The frequencies of watchedVideos by your friends are: 
B -> 1 
C -> 2

Example 2:

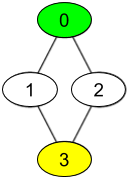
Input: watchedVideos = [["A","B"],["C"],["B","C"],["D"]], friends = [[1,2],[0,3],[0,3],[1,2]], id = 0, level = 2
Output: ["D"]
Explanation: 
You have id = 0 (green color in the figure) and the only friend of your friends is the person with id = 3 (yellow color in the figure).

 

Constraints:

  • n == watchedVideos.length == friends.length
  • 2 <= n <= 100
  • 1 <= watchedVideos[i].length <= 100
  • 1 <= watchedVideos[i][j].length <= 8
  • 0 <= friends[i].length < n
  • 0 <= friends[i][j] < n
  • 0 <= id < n
  • 1 <= level < n
  • if friends[i] contains j, then friends[j] contains i

Solution Explanation: 1311. Get Watched Videos by Your Friends

This problem requires finding the videos watched by friends at a specific level of distance from a given person. The most efficient approach is using Breadth-First Search (BFS).

Algorithm:

  1. Initialization:

    • Create a queue q to store the IDs of people to visit, starting with the given id.
    • Create a vis array (or set) to track visited people, initially marking the starting id as visited.
    • Create a cnt dictionary (or hash map) to store video frequencies.

  2. BFS Traversal:

    • Iterate level times. In each iteration:
      • Process all people currently in q. For each person:
        • Iterate through their friends (friends[i]).
        • If a friend is not yet visited (!vis[j]):
          • Mark the friend as visited (vis[j] = true).
          • Add the friend's ID to q.
    • After level iterations, q contains the IDs of all friends at the specified distance.

  3. Video Frequency Counting:

    • Iterate through the IDs in q. For each ID i:
      • Iterate through the videos watched by that person (watchedVideos[i]).
      • Increment the count of each video in the cnt dictionary.

  4. Sorting and Returning:

    • Convert the cnt dictionary's keys (videos) into a list.
    • Sort the list of videos based on their frequencies (ascending). If two videos have the same frequency, sort them alphabetically (ascending).
    • Return the sorted list of videos.

Time Complexity:

  • BFS traversal visits each person at most once, so it takes O(n) time, where n is the number of people.
  • Counting video frequencies takes O(v) time in the worst case, where v is the total number of videos watched by friends at the specified level.
  • Sorting the videos takes O(v log v) time.
  • Therefore, the overall time complexity is O(n + v + v log v), which simplifies to O(n + v log v).

Space Complexity:

  • The queue q stores at most n IDs.
  • The vis array takes O(n) space.
  • The cnt dictionary stores at most v entries.
  • Therefore, the overall space complexity is O(n + v).

Code Examples:

The code examples provided earlier in different languages (Python, Java, C++, Go, TypeScript) all implement this algorithm. They differ slightly in syntax and data structures used but share the same core logic. The efficiency of each implementation is consistent with the complexity analysis.