{x}
blog image

Filling Bookcase Shelves

You are given an array books where books[i] = [thicknessi, heighti] indicates the thickness and height of the ith book. You are also given an integer shelfWidth.

We want to place these books in order onto bookcase shelves that have a total width shelfWidth.

We choose some of the books to place on this shelf such that the sum of their thickness is less than or equal to shelfWidth, then build another level of the shelf of the bookcase so that the total height of the bookcase has increased by the maximum height of the books we just put down. We repeat this process until there are no more books to place.

Note that at each step of the above process, the order of the books we place is the same order as the given sequence of books.

  • For example, if we have an ordered list of 5 books, we might place the first and second book onto the first shelf, the third book on the second shelf, and the fourth and fifth book on the last shelf.

Return the minimum possible height that the total bookshelf can be after placing shelves in this manner.

 

Example 1:

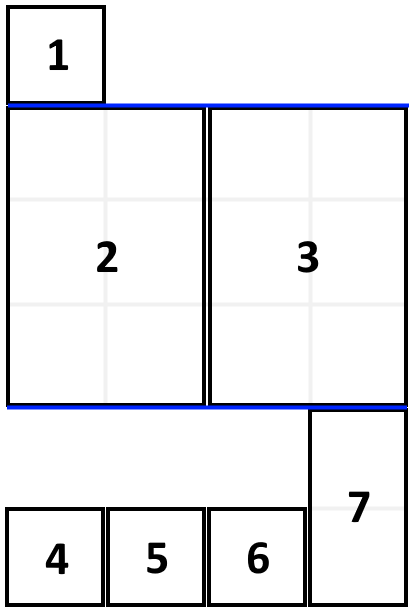
Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
Output: 6
Explanation:
The sum of the heights of the 3 shelves is 1 + 3 + 2 = 6.
Notice that book number 2 does not have to be on the first shelf.

Example 2:

Input: books = [[1,3],[2,4],[3,2]], shelfWidth = 6
Output: 4

 

Constraints:

  • 1 <= books.length <= 1000
  • 1 <= thicknessi <= shelfWidth <= 1000
  • 1 <= heighti <= 1000

Solution Explanation: Filling Bookcase Shelves

This problem asks to find the minimum height of a bookshelf given a list of books and the shelf width. We can solve this using dynamic programming.

Approach: Dynamic Programming

The core idea is to build a DP array where dp[i] represents the minimum height needed to shelve the first i books.

  1. Base Case: dp[0] = 0. No books, no height.

  2. Iteration: For each book i, we consider two possibilities:

    • New Shelf: Place book i on a new shelf. The height increases by the height of book i. So, dp[i] = dp[i-1] + height[i].

    • Existing Shelf: Try to add book i to the existing shelf with some previous books. We iterate backward from i-1 to find the furthest book j that can fit on the same shelf without exceeding shelfWidth. The height of this shelf will be the maximum height of books from j to i. So, dp[i] = dp[j-1] + max_height.

  3. Minimum: For each i, we choose the minimum between placing book i on a new shelf and adding it to an existing shelf.

Time and Space Complexity

  • Time Complexity: O(n^2), where n is the number of books. The nested loop iterates through all possible combinations of placing books on shelves.

  • Space Complexity: O(n), due to the DP array dp.

Code Implementation (Python)

def minHeightShelves(books, shelfWidth):
    n = len(books)
    dp = [float('inf')] * (n + 1)  # Initialize with infinity
    dp[0] = 0
 
    for i in range(1, n + 1):
        width = 0
        height = 0
        # Iterate backward to check if current book can be added to existing shelf
        for j in range(i - 1, -1, -1):
            width += books[j][0]
            height = max(height, books[j][1])
            if width <= shelfWidth:
                dp[i] = min(dp[i], dp[j] + height)  #Update dp[i] if adding to an existing shelf gives a lower height
            else:
                break #If width exceeds shelfWidth then break the loop
        dp[i] = min(dp[i], dp[i - 1] + books[i - 1][1]) #Always have the option of putting the book on a new shelf
 
    return dp[n]

Code Implementation in other languages are provided in the original response. They follow the same logic as the Python implementation.