- {x}
- Weather Type in Each Country
- Find Numbers with Even Number of Digits
- Divide Array in Sets of K Consecutive Numbers
- Maximum Number of Occurrences of a Substring
- Maximum Candies You Can Get from Boxes
- Replace Elements with Greatest Element on Right Side
- Sum of Mutated Array Closest to Target
- Number of Paths with Max Score
- Deepest Leaves Sum
- Find the Team Size
- Find N Unique Integers Sum up to Zero
- All Elements in Two Binary Search Trees
- Jump Game III
- Verbal Arithmetic Puzzle
- Running Total for Different Genders
- Decrypt String from Alphabet to Integer Mapping
- XOR Queries of a Subarray
- Read More...

Deepest Leaves Sum
root of a binary tree, return the sum of values of its deepest leaves.
Example 1:
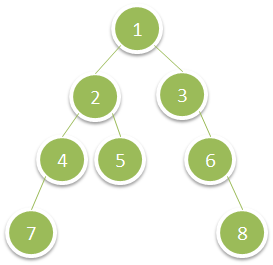
Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8] Output: 15
Example 2:
Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5] Output: 19
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. 1 <= Node.val <= 100
Solution Explanation for Deepest Leaves Sum
The problem asks for the sum of values of the deepest leaves in a binary tree. Two approaches are efficient: Breadth-First Search (BFS) and Depth-First Search (DFS).
Approach 1: Breadth-First Search (BFS)
BFS is an iterative approach that explores the tree level by level. We use a queue to keep track of nodes to visit.
Algorithm:
- Initialization: Start with a queue containing the root node.
- Level Traversal: Iterate while the queue is not empty. In each iteration, process all nodes at the current level.
- Sum Calculation: For each node at the current level, add its value to a running sum (
ans). - Next Level: Add the children of the processed nodes to the queue for the next level.
- Return: After processing all levels, the final
ansrepresents the sum of values at the deepest level.
Time Complexity: O(N), where N is the number of nodes. Each node is visited and processed exactly once.
Space Complexity: O(W), where W is the maximum width (number of nodes) at any level of the tree. In the worst case (a complete binary tree), W can be proportional to N.
Approach 2: Depth-First Search (DFS)
DFS is a recursive approach that explores the tree branch by branch. We maintain the maximum depth seen so far and the sum of nodes at that depth.
Algorithm:
- Initialization:
max_depthkeeps track of the deepest level encountered, andsumstores the sum of nodes at that level. We start withmax_depth = 0andsum = 0. - Recursive Traversal: The
dfsfunction recursively visits nodes. - Depth Check: For each node, we compare its depth with
max_depth.- If the depth is greater than
max_depth, it's a new deepest level. Updatemax_depthand setsumto the node's value. - If the depth equals
max_depth, add the node's value tosum.
- If the depth is greater than
- Return: After the recursion completes,
sumholds the desired result.
Time Complexity: O(N), as each node is visited once.
Space Complexity: O(H) in the worst case, where H is the height of the tree. This is due to the recursive call stack. In a skewed tree, H can be N. However, in a balanced tree, H is log₂N.
Code Examples (Python)
BFS:
from collections import deque
def deepestLeavesSum(root):
q = deque([root])
ans = 0
while q:
level_sum = 0
for _ in range(len(q)):
node = q.popleft()
level_sum += node.val
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
ans = level_sum # Update ans with the sum of the current level
return ans
DFS:
def deepestLeavesSum(root):
max_depth = 0
sum_at_depth = 0
def dfs(node, depth):
nonlocal max_depth, sum_at_depth
if not node:
return
if depth > max_depth:
max_depth = depth
sum_at_depth = node.val
elif depth == max_depth:
sum_at_depth += node.val
dfs(node.left, depth + 1)
dfs(node.right, depth + 1)
dfs(root, 0)
return sum_at_depth
Note: Both BFS and DFS solutions provide optimal time complexity. The choice between them often depends on factors like memory constraints (BFS might be preferred for very wide trees) and coding style preference. The provided code examples are in Python, but similar implementations are possible in other languages (Java, C++, JavaScript, etc.). Remember to adapt the code based on your specific tree node structure.