{x}
blog image

Count Sub Islands

You are given two m x n binary matrices grid1 and grid2 containing only 0's (representing water) and 1's (representing land). An island is a group of 1's connected 4-directionally (horizontal or vertical). Any cells outside of the grid are considered water cells.

An island in grid2 is considered a sub-island if there is an island in grid1 that contains all the cells that make up this island in grid2.

Return the number of islands in grid2 that are considered sub-islands.

 

Example 1:

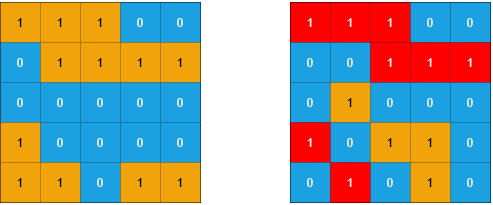
Input: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
Output: 3
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.

Example 2:

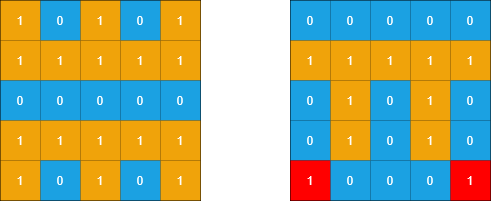
Input: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
Output: 2 
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.

 

Constraints:

  • m == grid1.length == grid2.length
  • n == grid1[i].length == grid2[i].length
  • 1 <= m, n <= 500
  • grid1[i][j] and grid2[i][j] are either 0 or 1.

1905. Count Sub Islands

Description

Given two binary matrices grid1 and grid2 of size m x n, where 1 represents land and 0 represents water, find the number of sub-islands in grid2. A sub-island in grid2 is an island whose cells are all also part of an island in grid1.

Solution: Depth-First Search (DFS)

This problem can be efficiently solved using Depth-First Search (DFS). The core idea is to iterate through grid2. Whenever we encounter a land cell (value 1), we initiate a DFS to explore the entire connected island. During this DFS, we simultaneously check if each cell in the island is also land in grid1. If even one cell in the grid2 island is water in grid1, the entire grid2 island is not a sub-island.

Algorithm

  1. Iterate: Traverse grid2 row by row and column by column.
  2. DFS Initiation: If a cell grid2[i][j] is 1 (land), start a DFS exploration from that cell.
  3. DFS Exploration:
    • Mark the current cell as visited in grid2 by setting it to 0.
    • Check if the corresponding cell in grid1 is also 1. If not, the island is not a sub-island, so we set isSubIsland to false.
    • Recursively explore the four adjacent cells (up, down, left, right).
  4. Sub-island Check: After the DFS for a connected component completes, if isSubIsland is still true, increment the count of sub-islands.

Time and Space Complexity

  • Time Complexity: O(M * N), where M and N are the dimensions of the grid. We visit each cell at most once.
  • Space Complexity: O(M * N) in the worst case, due to the recursive call stack of the DFS. In practice, it could be less depending on the structure of the islands.

Code (Python)

def countSubIslands(grid1, grid2):
    m, n = len(grid1), len(grid1[0])
    count = 0
 
    def dfs(i, j):
        if not (0 <= i < m and 0 <= j < n and grid2[i][j] == 1):
            return True  # Base case: out of bounds or water
 
        grid2[i][j] = 0  # Mark as visited
 
        is_sub_island = grid1[i][j] == 1  # Check if this cell is land in grid1
 
        is_sub_island &= dfs(i + 1, j)  # Explore down
        is_sub_island &= dfs(i - 1, j)  # Explore up
        is_sub_island &= dfs(i, j + 1)  # Explore right
        is_sub_island &= dfs(i, j - 1)  # Explore left
 
        return is_sub_island
 
    for i in range(m):
        for j in range(n):
            if grid2[i][j] == 1:
                if dfs(i, j):
                    count += 1
 
    return count

The code in other languages (Java, C++, Go, TypeScript, JavaScript) follows a very similar structure, using the same DFS logic. The primary difference would be in syntax and data structure handling specific to each language. The core algorithm remains the same.