{x}
blog image

Count Pairs Of Nodes

You are given an undirected graph defined by an integer n, the number of nodes, and a 2D integer array edges, the edges in the graph, where edges[i] = [ui, vi] indicates that there is an undirected edge between ui and vi. You are also given an integer array queries.

Let incident(a, b) be defined as the number of edges that are connected to either node a or b.

The answer to the jth query is the number of pairs of nodes (a, b) that satisfy both of the following conditions:

  • a < b
  • incident(a, b) > queries[j]

Return an array answers such that answers.length == queries.length and answers[j] is the answer of the jth query.

Note that there can be multiple edges between the same two nodes.

 

Example 1:

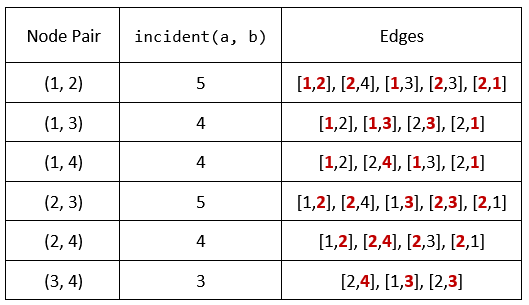
Input: n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
Output: [6,5]
Explanation: The calculations for incident(a, b) are shown in the table above.
The answers for each of the queries are as follows:
- answers[0] = 6. All the pairs have an incident(a, b) value greater than 2.
- answers[1] = 5. All the pairs except (3, 4) have an incident(a, b) value greater than 3.

Example 2:

Input: n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
Output: [10,10,9,8,6]

 

Constraints:

  • 2 <= n <= 2 * 104
  • 1 <= edges.length <= 105
  • 1 <= ui, vi <= n
  • ui != vi
  • 1 <= queries.length <= 20
  • 0 <= queries[j] < edges.length

Solution Explanation: Count Pairs of Nodes

This problem asks to count pairs of nodes (a, b) where a < b and the number of edges incident to either a or b exceeds a given query value. The solution uses a combination of counting, sorting, and binary search for efficiency.

Approach:

  1. Edge Counting: We first create a cnt array to store the degree (number of incident edges) of each node. A hash map g stores the number of edges between each pair of nodes (to account for multiple edges between the same nodes). This step iterates through the edges array.

  2. Sorting: The cnt array is sorted to efficiently find pairs satisfying the incident edge condition.

  3. Query Processing: For each query q in queries:

    • We iterate through each node a.
    • Using binary search on the sorted cnt array, we find the number of nodes b (where b > a) such that cnt[a] + cnt[b] > q. This efficiently identifies pairs that meet the incident edge condition.
    • We adjust the count to account for cases where multiple edges between the same pair of nodes cause the condition to be met.

Time Complexity:

  • Edge Counting: O(E), where E is the number of edges.
  • Sorting: O(N log N), where N is the number of nodes.
  • Query Processing: O(Q * N * log N), where Q is the number of queries. The binary search within the inner loop contributes to the log N factor.

Therefore, the overall time complexity is O(E + N log N + Q * N * log N). In the worst case, where Q is large, the query processing dominates.

Space Complexity:

  • cnt array: O(N)
  • g hash map: O(E) in the worst case (if all edges are unique).

The overall space complexity is O(N + E).

Code (Python):

from collections import defaultdict
from bisect import bisect_right
 
class Solution:
    def countPairs(self, n: int, edges: list[list[int]], queries: list[int]) -> list[int]:
        cnt = [0] * n
        g = defaultdict(int)
        for a, b in edges:
            a, b = a - 1, b - 1
            a, b = min(a, b), max(a, b)
            cnt[a] += 1
            cnt[b] += 1
            g[(a, b)] += 1
 
        s = sorted(cnt)
        ans = [0] * len(queries)
        for i, t in enumerate(queries):
            for j, x in enumerate(s):
                k = bisect_right(s, t - x, lo=j + 1)
                ans[i] += n - k
            for (a, b), v in g.items():
                if cnt[a] + cnt[b] > t and cnt[a] + cnt[b] - v <= t:
                    ans[i] -= 1
        return ans

The code in other languages (Java, C++, Go, TypeScript) follows a similar structure and logic, adapting the syntax and data structures appropriately for each language. The core algorithm remains consistent across all implementations.