- {x}
- Flood Fill
- Sentence Similarity
- Asteroid Collision
- Parse Lisp Expression
- Sentence Similarity II
- Monotone Increasing Digits
- Daily Temperatures
- Delete and Earn
- Cherry Pickup
- Closest Leaf in a Binary Tree
- Network Delay Time
- Find Smallest Letter Greater Than Target
- Prefix and Suffix Search
- Min Cost Climbing Stairs
- Largest Number At Least Twice of Others
- Shortest Completing Word
- Contain Virus
- Read More...

Cherry Pickup
You are given an n x n grid representing a field of cherries, each cell is one of three possible integers.
0means the cell is empty, so you can pass through,1means the cell contains a cherry that you can pick up and pass through, or-1means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:
- Starting at the position
(0, 0)and reaching(n - 1, n - 1)by moving right or down through valid path cells (cells with value0or1). - After reaching
(n - 1, n - 1), returning to(0, 0)by moving left or up through valid path cells. - When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell
0. - If there is no valid path between
(0, 0)and(n - 1, n - 1), then no cherries can be collected.
Example 1:
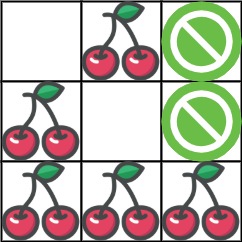
Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]] Output: 5 Explanation: The player started at (0, 0) and went down, down, right right to reach (2, 2). 4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]]. Then, the player went left, up, up, left to return home, picking up one more cherry. The total number of cherries picked up is 5, and this is the maximum possible.
Example 2:
Input: grid = [[1,1,-1],[1,-1,1],[-1,1,1]] Output: 0
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 50grid[i][j]is-1,0, or1.grid[0][0] != -1grid[n - 1][n - 1] != -1
Solution Explanation: Cherry Pickup
This problem involves finding the maximum number of cherries that can be collected by traversing an n x n grid twice: once from (0,0) to (n-1, n-1), and then back to (0,0). The key constraint is that movement is restricted to right or down during the first traversal and left or up during the second. The grid contains 0 (empty), 1 (cherry), and -1 (thorn).
Approach: Dynamic Programming
The optimal solution uses dynamic programming to efficiently explore the state space of possible paths. Instead of thinking of two separate traversals, it's more efficient to consider the two robots moving simultaneously.
State Representation:
We use a 3D DP array f[k][i1][i2]. This represents the maximum number of cherries collected after k steps, where:
k: The total number of steps taken by both robots. The range is from 0 to 2n-2 (inclusive).i1: The row index of the first robot.i2: The row index of the second robot.
The column index of each robot can be easily derived as k - i1 and k - i2 respectively.
Base Case:
f[0][0][0] = grid[0][0] because at the beginning, both robots are at (0,0).
State Transition:
For each step k, we iterate through all possible positions i1 and i2 for the two robots. From the previous step k-1, the robots can move from (x1, k-1-x1) and (x2, k-1-x2) to (i1, k-i1) and (i2, k-i2) respectively. x1 and x2 are the previous row positions. There are four possible movements from the previous step:
- Both robots move down (x1 = i1 - 1, x2 = i2 - 1)
- Robot 1 moves down, Robot 2 moves right (x1 = i1 - 1, x2 = i2)
- Robot 1 moves right, Robot 2 moves down (x1 = i1, x2 = i2 -1)
- Both robots move right (x1 = i1, x2 = i2)
We calculate the cherries collected at the current positions (i1, k-i1) and (i2, k-i2), adding them (unless they're at the same position). We then update f[k][i1][i2] with the maximum value considering all possible movements from the previous step.
Final Result:
The maximum number of cherries collected is f[2n-2][n-1][n-1]. We take the maximum of 0 and this value to handle cases where no path exists.
Time and Space Complexity
- Time Complexity: O(n³). The three nested loops iterate through all possible states.
- Space Complexity: O(n³). The DP array
frequires O(n³) space.
Code (Python)
class Solution:
def cherryPickup(self, grid: List[List[int]]) -> int:
n = len(grid)
f = [[[-float('inf')] * n for _ in range(n)] for _ in range(2 * n - 1)]
f[0][0][0] = grid[0][0]
for k in range(1, 2 * n - 1):
for i1 in range(n):
for i2 in range(n):
j1, j2 = k - i1, k - i2
if not (0 <= j1 < n and 0 <= j2 < n and grid[i1][j1] != -1 and grid[i2][j2] != -1):
continue
t = grid[i1][j1]
if i1 != i2:
t += grid[i2][j2]
for x1 in range(max(0, i1 - 1), min(i1 + 1, n)):
for x2 in range(max(0, i2 - 1), min(i2 + 1, n)):
f[k][i1][i2] = max(f[k][i1][i2], f[k - 1][x1][x2] + t)
return max(0, f[2 * n - 2][n - 1][n - 1])The code in other languages (Java, C++, Go, Typescript, Javascript) follows a similar structure and logic, implementing the dynamic programming approach explained above. The minor differences arise from language-specific syntax and data structure handling.