- {x}
- The Number of Seniors and Juniors to Join the Company II
- Final Value of Variable After Performing Operations
- Sum of Beauty in the Array
- Detect Squares
- Longest Subsequence Repeated k Times
- Average Height of Buildings in Each Segment
- Maximum Difference Between Increasing Elements
- Grid Game
- Check if Word Can Be Placed In Crossword
- The Score of Students Solving Math Expression
- Number of Accounts That Did Not Stream
- Brightest Position on Street
- Convert 1D Array Into 2D Array
- Number of Pairs of Strings With Concatenation Equal to Target
- Maximize the Confusion of an Exam
- Maximum Number of Ways to Partition an Array
- Low-Quality Problems
- Read More...

Check if Word Can Be Placed In Crossword
You are given an m x n matrix board, representing the current state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), ' ' to represent any empty cells, and '#' to represent any blocked cells.
A word can be placed horizontally (left to right or right to left) or vertically (top to bottom or bottom to top) in the board if:
- It does not occupy a cell containing the character
'#'. - The cell each letter is placed in must either be
' '(empty) or match the letter already on theboard. - There must not be any empty cells
' 'or other lowercase letters directly left or right of the word if the word was placed horizontally. - There must not be any empty cells
' 'or other lowercase letters directly above or below the word if the word was placed vertically.
Given a string word, return true if word can be placed in board, or false otherwise.
Example 1:
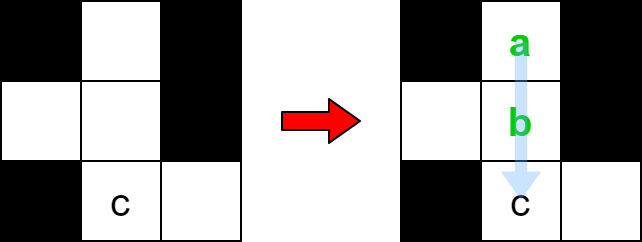
Input: board = [["#", " ", "#"], [" ", " ", "#"], ["#", "c", " "]], word = "abc" Output: true Explanation: The word "abc" can be placed as shown above (top to bottom).
Example 2:
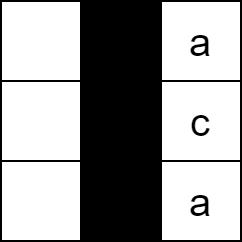
Input: board = [[" ", "#", "a"], [" ", "#", "c"], [" ", "#", "a"]], word = "ac" Output: false Explanation: It is impossible to place the word because there will always be a space/letter above or below it.
Example 3:
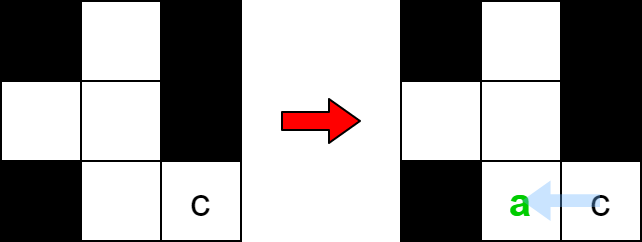
Input: board = [["#", " ", "#"], [" ", " ", "#"], ["#", " ", "c"]], word = "ca" Output: true Explanation: The word "ca" can be placed as shown above (right to left).
Constraints:
m == board.lengthn == board[i].length1 <= m * n <= 2 * 105board[i][j]will be' ','#', or a lowercase English letter.1 <= word.length <= max(m, n)wordwill contain only lowercase English letters.
Solution Explanation: Check if Word Can Be Placed In Crossword
This problem asks whether a given word can be placed in a crossword puzzle board. The board contains empty spaces (' '), blocked cells ('#'), and possibly existing letters. The word can be placed horizontally (left-to-right or right-to-left) or vertically (top-to-bottom or bottom-to-top). The placement must adhere to these rules:
- No '#' cells: The word cannot occupy any '#' cells.
- Matching existing letters: Empty cells (' ') can be occupied. Existing letters must match the corresponding letter in the word.
- Boundary conditions: If placed horizontally, there must be '#' or board boundaries on both sides of the word. The same applies vertically; there must be '#' or board boundaries above and below the word.
Approach: Enumeration and Boundary Check
The most efficient approach is to enumerate all possible starting positions and orientations of the word on the board and check for validity.
1. Iterate through board: The algorithm iterates through each cell of the board as a potential starting point for the word.
2. Check four orientations: For each starting position, it checks four possible orientations:
- Horizontal (left-to-right)
- Horizontal (right-to-left)
- Vertical (top-to-bottom)
- Vertical (bottom-to-top)
3. Boundary check: Before attempting placement, the algorithm checks if the chosen orientation respects boundary conditions. A word cannot be placed if there are empty spaces or letters adjacent to it in the direction of placement. For example, for horizontal placement, the cells immediately to the left and right of the starting position should be '#' or outside the board.
4. Character matching: The algorithm iterates through the letters of the word and checks if they match existing letters on the board or are placed in empty cells. If a mismatch occurs or a '#' cell is encountered, the current orientation is invalid.
5. Return true if valid placement is found: If any valid placement is found, the algorithm returns true. Otherwise, it returns false after checking all positions and orientations.
Time Complexity Analysis
- The outer loop iterates through all cells of the board, which takes O(m*n) time where 'm' is the number of rows and 'n' is the number of columns.
- For each cell, the algorithm checks four orientations.
- Checking each orientation involves iterating through the word (length 'k'), so this part takes O(k) time.
- Therefore, the overall time complexity is O(m * n * k).
Space Complexity Analysis
The algorithm uses a constant amount of extra space to store variables and function parameters. Therefore, the space complexity is O(1).
Code Implementation (Python)
def placeWordInCrossword(board, word):
m, n = len(board), len(board[0])
k = len(word)
def is_valid(r, c, dr, dc):
nr, nc = r + dr * k, c + dc * k
if 0 <= nr < m and 0 <= nc < n and board[nr][nc] != '#':
return False
for i in range(k):
curr_r, curr_c = r + i * dr, c + i * dc
if not (0 <= curr_r < m and 0 <= curr_c < n):
return False
if board[curr_r][curr_c] != ' ' and board[curr_r][curr_c] != word[i]:
return False
return True
for r in range(m):
for c in range(n):
if is_valid(r, c, 0, 1) or is_valid(r, c, 0, -1) or \
is_valid(r, c, 1, 0) or is_valid(r, c, -1, 0):
return True
return False
The code in other languages (Java, C++, Go) follows a very similar structure, implementing the same logic with minor syntactic differences. The is_valid function encapsulates the checks for boundary conditions and character matching for a given position and orientation.