- {x}
- Number of Recent Calls
- Shortest Bridge
- Knight Dialer
- Stamping The Sequence
- Reorder Data in Log Files
- Range Sum of BST
- Minimum Area Rectangle
- Distinct Subsequences II
- Valid Mountain Array
- DI String Match
- Find the Shortest Superstring
- Delete Columns to Make Sorted
- Minimum Increment to Make Array Unique
- Validate Stack Sequences
- Most Stones Removed with Same Row or Column
- Bag of Tokens
- Largest Time for Given Digits
- Read More...

Valid Mountain Array
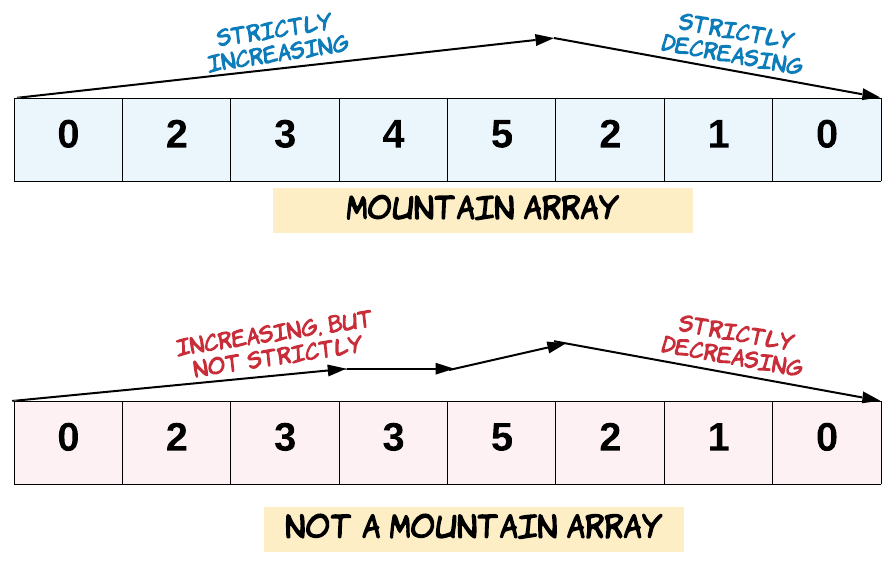
Given an array of integers arr, return true if and only if it is a valid mountain array.
Recall that arr is a mountain array if and only if:
arr.length >= 3- There exists some
iwith0 < i < arr.length - 1such that:arr[0] < arr[1] < ... < arr[i - 1] < arr[i]arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
Example 1:
Input: arr = [2,1] Output: false
Example 2:
Input: arr = [3,5,5] Output: false
Example 3:
Input: arr = [0,3,2,1] Output: true
Constraints:
1 <= arr.length <= 1040 <= arr[i] <= 104
Solution Explanation: Valid Mountain Array
The problem asks to determine if an array represents a valid mountain. A valid mountain array must satisfy these conditions:
- Length: The array's length must be at least 3.
- Increasing then Decreasing: There must be a peak index
i(0 < i < arr.length - 1) such that the elements strictly increase up to indexiand strictly decrease from indexionwards.
Approach: Two Pointers
The most efficient approach uses two pointers, one starting from the left (i) and the other from the right (j).
-
Initial Check: We first verify if the array length is less than 3. If so, it cannot be a mountain array, and we return
false. -
Left Pointer (Ascending Phase): The left pointer
iiterates to the right as long as the elements are strictly increasing (arr[i] < arr[i+1]). This continues until we reach a point where the increasing trend stops. -
Right Pointer (Descending Phase): The right pointer
jiterates to the left as long as the elements are strictly decreasing (arr[j] > arr[j-1]). This continues until we find the end of the decreasing section. -
Peak Check: If both pointers stop at the same index (
i == j), this signifies a valid mountain where the peak is at indexi(orj). Ifi != j, the array doesn't satisfy the condition of being a mountain.
Time and Space Complexity Analysis
- Time Complexity: O(n), where n is the length of the array. Both pointers traverse the array at most once.
- Space Complexity: O(1). The algorithm uses a constant amount of extra space, regardless of the input array size.
Code Implementation (Python)
class Solution:
def validMountainArray(self, arr: List[int]) -> bool:
n = len(arr)
if n < 3:
return False
i = 0
while i + 1 < n and arr[i] < arr[i+1]:
i += 1
j = n - 1
while j -1 >= 0 and arr[j] < arr[j-1]:
j -= 1
return i == j and i != 0 and j != n-1 #Check for peak and not being flat lineThe added condition i != 0 and j != n-1 in the return statement ensures that the peak isn't at either the start or the end of the array; a necessary condition for a true mountain.
Code Implementations in Other Languages
The logic remains the same across different programming languages. The variations below primarily involve syntax changes:
Java:
class Solution {
public boolean validMountainArray(int[] arr) {
int n = arr.length;
if (n < 3) return false;
int i = 0;
while (i + 1 < n && arr[i] < arr[i + 1]) i++;
int j = n - 1;
while (j - 1 >= 0 && arr[j] < arr[j - 1]) j--;
return i == j && i != 0 && j != n - 1;
}
}C++:
class Solution {
public:
bool validMountainArray(vector<int>& arr) {
int n = arr.size();
if (n < 3) return false;
int i = 0;
while (i + 1 < n && arr[i] < arr[i + 1]) i++;
int j = n - 1;
while (j - 1 >= 0 && arr[j] < arr[j - 1]) j--;
return i == j && i != 0 && j != n - 1;
}
};Go:
func validMountainArray(arr []int) bool {
n := len(arr)
if n < 3 {
return false
}
i := 0
for i+1 < n && arr[i] < arr[i+1] {
i++
}
j := n - 1
for j-1 >= 0 && arr[j] < arr[j-1] {
j--
}
return i == j && i != 0 && j != n-1
}JavaScript:
const validMountainArray = (arr) => {
const n = arr.length;
if (n < 3) return false;
let i = 0;
while (i + 1 < n && arr[i] < arr[i + 1]) i++;
let j = n - 1;
while (j - 1 >= 0 && arr[j] < arr[j - 1]) j--;
return i === j && i !== 0 && j !== n - 1;
};These examples demonstrate the adaptability of the two-pointer approach across various programming languages. The core algorithm remains consistent, showcasing its efficiency and elegance in solving the valid mountain array problem.