- {x}
- Find the Closest Palindrome
- Array Nesting
- Reshape the Matrix
- Permutation in String
- Maximum Vacation Days
- Median Employee Salary
- Managers with at Least 5 Direct Reports
- Find Median Given Frequency of Numbers
- Subtree of Another Tree
- Squirrel Simulation
- Winning Candidate
- Distribute Candies
- Out of Boundary Paths
- Employee Bonus
- Get Highest Answer Rate Question
- Find Cumulative Salary of an Employee
- Count Student Number in Departments
- Read More...

Subtree of Another Tree
Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.
A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.
Example 1:
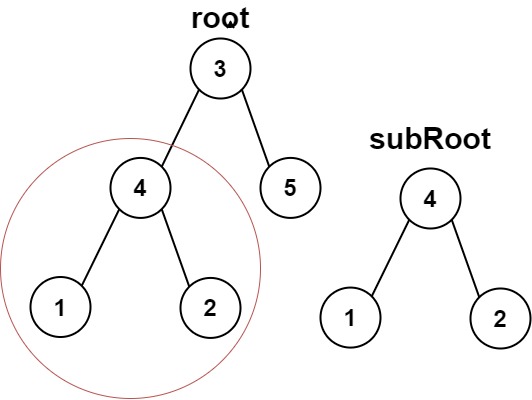
Input: root = [3,4,5,1,2], subRoot = [4,1,2] Output: true
Example 2:
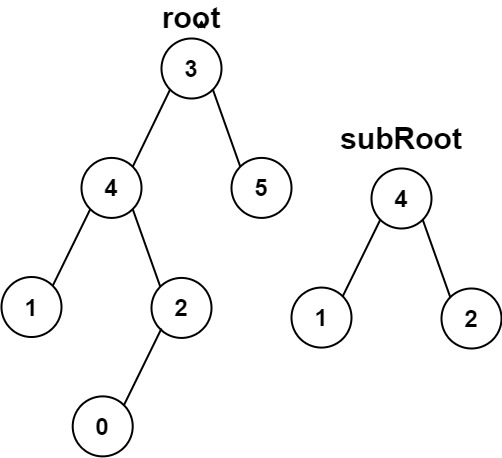
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] Output: false
Constraints:
- The number of nodes in the
roottree is in the range[1, 2000]. - The number of nodes in the
subRoottree is in the range[1, 1000]. -104 <= root.val <= 104-104 <= subRoot.val <= 104
Solution Explanation: Subtree of Another Tree
This problem asks whether one binary tree (subRoot) is a subtree of another binary tree (root). A subtree is a node in the larger tree and all of its descendants. The solution uses Depth-First Search (DFS).
Approach
The core idea is to recursively check if subRoot exists within root. This is done in two steps:
-
same(p, q)function: This helper function compares two trees (rooted at nodespandq) for structural and value equality. It returnstrueif they are identical, andfalseotherwise. The base case is when eitherporqisnull; they are only equal if both arenull. Otherwise, it recursively checks if the root values are equal and if their left and right subtrees are also equal. -
isSubtree(root, subRoot)function: This function recursively searches forsubRootwithinroot.- Base case: If
rootisnull, it returnsfalse(because a null tree cannot contain another tree). - It first checks if
rootandsubRootare the same usingsame(root, subRoot). If they are, it returnstrue. - Otherwise, it recursively calls
isSubtreeon the left and right subtrees ofroot, continuing the search. If either recursive call findssubRoot, it returnstrue. If neither finds it, it returnsfalse.
- Base case: If
Code Examples (Python)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
def same(p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if p is None or q is None:
return p is q # Both None or both not None
return p.val == q.val and same(p.left, q.left) and same(p.right, q.right)
if root is None:
return False
return (
same(root, subRoot)
or self.isSubtree(root.left, subRoot)
or self.isSubtree(root.right, subRoot)
)
Time and Space Complexity Analysis
-
Time Complexity: O(m * n), where 'n' is the number of nodes in
rootand 'm' is the number of nodes insubRoot. In the worst case,samefunction might be called for every node inroot, and each call tosametakes O(m) time to compare the structure ofsubRoot. -
Space Complexity: O(n) in the worst case, due to the recursive call stack depth which can be equal to the height of the
roottree. The space used by thesamefunction is O(m) but is reused in each recursive call.
The other language examples follow the same algorithmic approach, differing only in syntax. The time and space complexity remain consistent across all implementations.